A positively charged infinitely long cylinder has a radius of 0.1 m and surface charge density of 8.85×10−12C/m2. What is the intensity of the electric field at a point on the surface of the cylinder, if the cylinder is kept in vacuum?
0.5 V/m
1 V/m
1.5 V/m
2 V/m
The correct Answer is:B
E=σRrε0k but r=R
∴E=σε0k=8.85×10−128.85×10−12=1Vm
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP20videos
ELECTROSTATICS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
Similar Questions
A uniformaly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0μC/m2
Find the charge on the sphere.
(b) What is the total electric flux leaving the surface of the sphere?View SolutionAn infinite cylinder of radius r with surface charge density σ is rotated about its central axis with angular speed ω. Then the magnetic field at any point inside the cylinder is
View Solution
Knowledge Check
- Question 1 - Select One
The energy density at a point in vacuum is 1.77×10−7J/m3. The intensity of the electric field at the point is
A100V/mB200V/mC300V/mD400V/m - Question 2 - Select One
Find the electric field intensity due to a positively charged conducting cylinder with radius 1 cm and surface charge density 10−9C/m2, at a point at a distance of 2 m from the axis of cylinder. The dielectric constant of the medium surrounding the cylinder is 2.
A0.28V/mB1.28V/mC2.28V/mD1.00V/m - Question 3 - Select One
A charged cylinder of radius 2 cm has surface density of charge 8.85×10−9C/m2. It is placed in a medium of dielectric constant 5. The electric intensity at a point at a distance of 4 m from its axis is
A5V/mB4V/mC3V/mD1V/m
An infinitely long time charge has linear charge density λC/m the line charge is along the line x=0,z=2m find the electric field at point (1,1,1) m.
View SolutionA uniformly charged conducting sphere of 2.4m diameter has a surface density of 80.0μC/m2. (a) Find the charge on the sphere (b) What is the total electric flux leaving the surface of the sphere ?
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
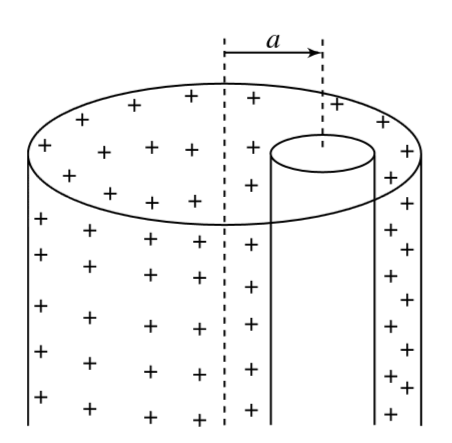 View Solution
View SolutionAn infinite line charge is at the axis of a cylinder of length 1 m and radius 7 cm. If electric field at any point on the curved surface of cylinder is 250 NC−1, then net electric flux through the cylinder is
View SolutionThe intensity of the electric field at a pont close but outside a charged conducting cylinder is proportional to (r is the distance of the point from the axis of the cylinder)
View Solution

