A positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.

2qEm(√lg)
qEm(√l√g)
qEm(√2lg)
qE2m(√lg)
The correct Answer is:B
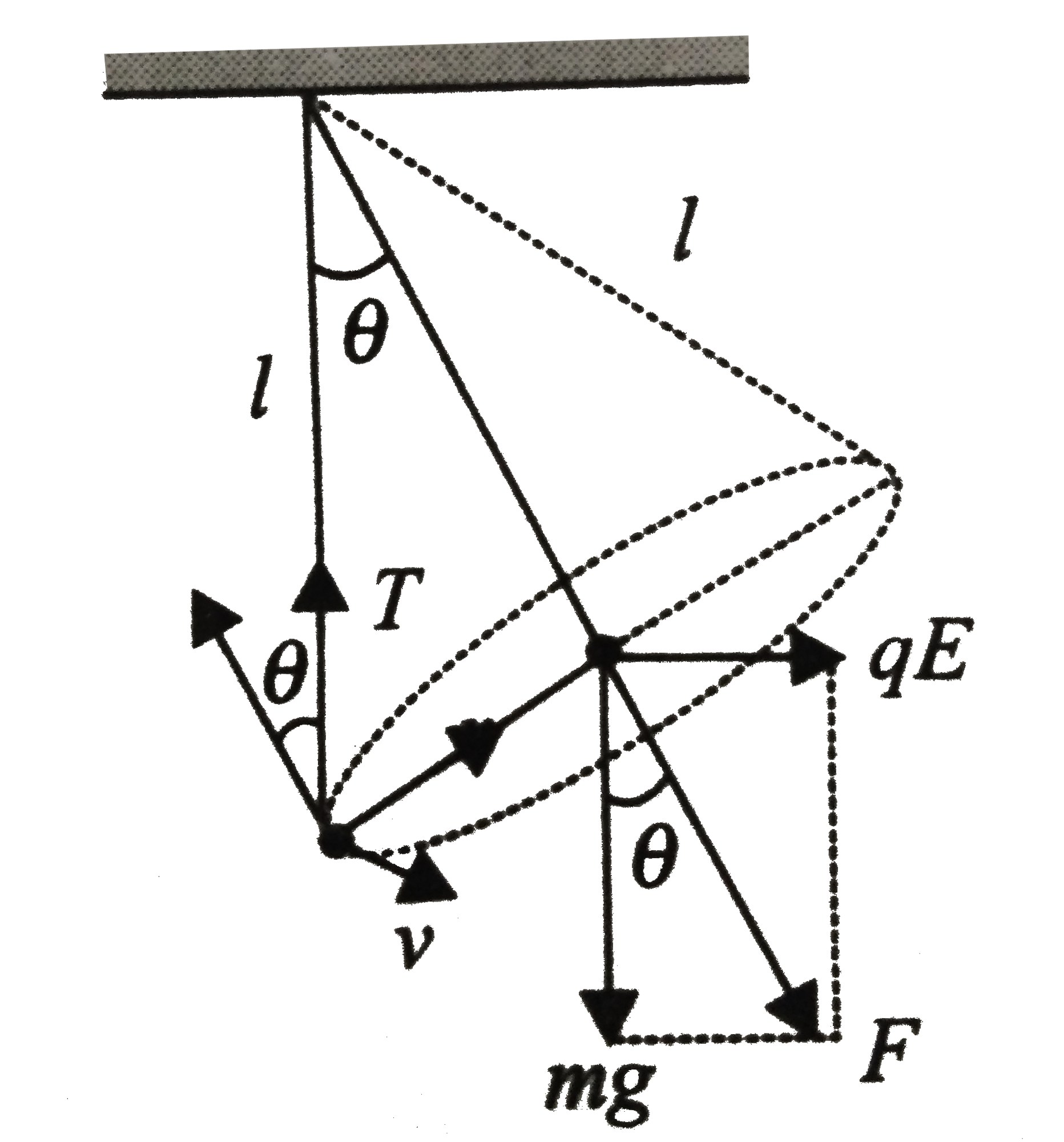
b. θ is equilibrium position. Net force in equilibrium position
F=√(mg)2+(qE)2
tanθ=qEmg
Tcosθ=F
Tsinθ=mv2r
where r=lsinθ
Solve to get v=qEm√lg
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
A particle of mass m=0.1kg and having positive charge q=75μC is suspended from a point by a thread of length l=10cm. In the space, a uniform horizontal electric field E=104NC−1 exists. The particle is drawn aside so that the thread becomes vertical and then it is projected horizontally with velocity v such that the particle starts to move along a circle with the same constant speed V. Calculate the radius of the circle and speed v(g=10ms−2).
View SolutionA particle of charge q is projected from point P with velocity v as shown. Choose the correct statement from the following.

View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).

View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionA particle of charge q0 and of mass m0 is projected along the y-axis at t=0 from origin with a velocity V0. If a uniform electric field E0 also exist along the x-axis, then the time at which debroglie wavelength of the particle becomes half of the initial value is:
View SolutionA heavy particle hanging from a string of length I is projected horizontally with speed √gl . Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View SolutionA particle of charge q and mass m is projected from the origin with velocity v=v0ˆi in a non uniformj magnetic fiedl B=−B0xˆk. Here v0 and B0 are positive constants of proper dimensions. Find the maximum positive x coordinate of the particle during its motion.
View Solution
