A projectile is fired horizontally with a velocity u making an angle θ . Derive the expression for time of the flight . Solution in Tamil
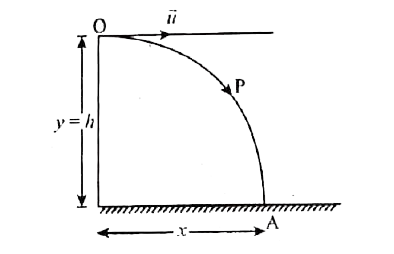
Let us consider a projectile, that is, thrown horizontal with an initial velocity →u from the top of a tower of height h in the figure .
Motion along horizontal direction : The particle has zero acceleration along x direction. So, the initial velocity u(x) remains constant throughout the motion. The distance traveled by the projectile at a time t is given by x=uxt+12at2
Since a = 0 along x direction, we get
x=uxt ...(1)
Motion along downward direction : Here uy=0 (initial velocity has no downward component), a = g .The distance y at time y is given by
y=uyt+12at2 , we get
y=12gt2 [u = 0, a = g] . . . (2)
Substituting the value of t from equation (1) in equation (2) we have
y=12gx2u2x=(g2u2x)x2
y=Kx2 ...(3)
Where K=g2u2x is a constant of proportionality .
Equation (3) gives the trajectory of the projectile. Thus , the path followed by the projectile is a parabola .
Time of Flight : The time taken for the projectile to complete its trajectory . It is also time taken by the projectile to hit the ground .
Consider a tower and a projectile . Let h be the height of a tower . Let T be the time taken by the projectile to hit the ground, after being thrown horizontally from the tower .
We know that sy=uyt+12at2 for vertical motion . Here sy=h,t=T (since there is no initial vertical velocity uy=0
∴h=12gT2(or)T=√2hg
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (V. Numerical problems).166videos
KINEMATICS
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINEMATICS EXERCISE - Other important questions & answers (III. Short answer questions).26videos
KINEMATICS
- BOOK - PREMIERS PUBLISHERSCHAPTER - GRAVITATIONEXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (CONCEPTUAL QUESTIONS)34videos
GRAVITATION
- BOOK - PREMIERS PUBLISHERSCHAPTER - KINETIC THEORY OF GASESEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (VI. Conceptual Questions.)8videos
KINETIC THEORY OF GASES
Similar Questions
A crow is sitting on a branch of tree whose co-ordinates are (1,2,3) . A hunter is standing on the ground . Represent the position of the crow with respect to the hunter .
03:41View SolutionWrite note on function with example.
05:10View SolutionWhy a body weighs less at the equator than at the poles?
03:01View SolutionWhen an automobile travels for a long distance , the air pressure in the tyres increases slightly . Why ?
03:01View SolutionA projectile is fired with a velocity u at right angles to the slope, which is inclined at an angle θ with the horizontal. Derive an expression for the distance R to the point of impact.
 . 07:08View Solution
. 07:08View SolutionA projectile is fired horizontally with a velocity u . Show that its trajectory is a parabola. Also obtain the expression for Time of flight .
View SolutionA projectile is fired horizontally with a velocity u making an angle θ . Derive the expression for time of the flight .
View SolutionA projectile is fired horizontally with a velocity u making an angle θ . Derive the expression for time of the flight .
07:22View SolutionWhat is a projectile ? Obtain an expression for: maximum height , time of flight and the horizontal range when a projectile is fired at an angle theta with the horizontal.
04:21View SolutionA projectile fired with velocity u at right angle to the slope which is inclined at an angle θ with horizontal. The expression for R is
03:56View SolutionA projectile fired with velocity u at right angle to theslope which is inclined at an angle θ with horizontal. The expression for R is
06:58View SolutionFor a projectile first with velocity u at an angle θ with the horizontal.
 View Solution
View SolutionA projectile is fired with a velocity 'u' making an angle theta with the horizontal. Show that its trajectory is a parabola.
View SolutionA projectile is projected with velocity u making angle θ with horizontal direction, find : time of flight.
View SolutionA projectile is fired at an angle θ with the horizontal with velocity u. Deduce the expression for the maximum height reached by it.
07:15View SolutionA projectile fired with velocity u at right angle to the slope which is inclined at an angle theta with horizontal. The expression for R is
12:06View Solution

