A pulley-rope-mass arrangement is shown in fig. Find the acceleration of block m1 when the masses are set free to move. Assume that the pulley and the ropes are ideal.
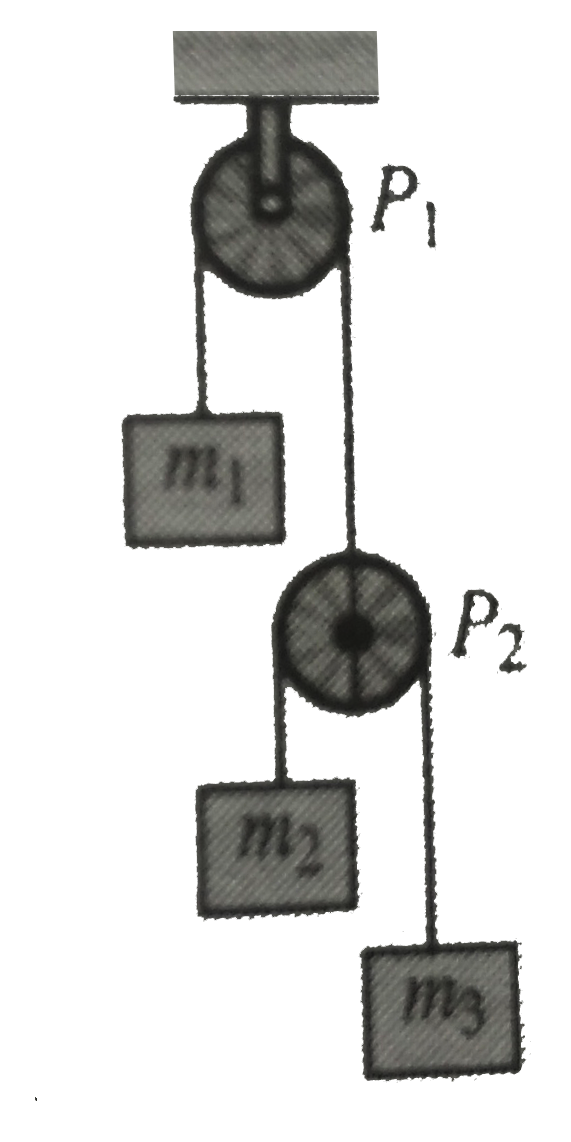
Appling the equations of motion for pulleys and blocks
For m1:T−m1g=m1a1 ….(i)
For m2:m2g−T2=m2a2 …(ii)
For pulley P1:2T−T=0×ap1
For pulley P2:T2−T=0×ap2 …(iv)
From Eq (iii), T=0, from (iv), T2=0 and from (i) and (ii). a1=−g , also a2=g. Hence, blocks m1 and m2 both will move down with acceleration g downward direction.
Calculating aP1 and aP2
Constraint relations: Consider the reference line and the position vectors of the pulley and masses as shown in fig .write the length of the rope in terms of position vector and differentiate it to obtain the relation between acceleration of the masses and pulleys.

* For the length of the string connecting P2 and m2 not to change and for this rope not to slacken, ap2=a2=g.
* Length of the string connecting P1 to m1 not to change and for this rope not to slacken:
l=(x1−xP1)+xP1+(xP2−xP1)+xP2
=x1−xP1+xP2
Differentiating this equation w.r.t twice we get
d2ldt2=d2x1dt2−d2xP1dt2+2d2xP2dt2⇒0=a1−aP1−2aP2
⇒0=g−aP1+2g⇒aP1=3g.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
Find the acceleration blocks in fig. The pulley and the string are massless.
 View Solution
View SolutionConsider the arrangement shown in the figure. Find the acceleration of the block
(a) A monkey moves upward with respect to the rope with acceleration a0
(b) A monkey moves downward with respect to the rope with acceleration a0
Assume the surface smooth, pulley and string light.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Find the acceleration of the block of mass m. Assume pulleys are massless and frictionless.
 Ag/3B2g3Cg2DNone
Ag/3B2g3Cg2DNone - Question 2 - Select One
In the arrangement shown, the pulleys and the string are ideal. The acceleration of block B is.
 Ag/5Bg/2C2g/5D2g/3
Ag/5Bg/2C2g/5D2g/3 - Question 3 - Select One
In the arrangement shown, the mass m will ascend with an acceleration ( Pulley and rope are massless)
 AzeroBg5CgD2g
AzeroBg5CgD2g
Two monkeys A and B of equal mass 'm' can climb strings of a pulley arrangement as shown in figure.Find magnitude of acceleration in m/s^(2) of A with respect to rope so that the block remains stationary.It is given that B is just holding the string.Assume pulley is frictionless and string is massless and inextensible.
View SolutionThe velocities of A and B shown in fig. Find the speed (in ms−1) of block C. (Assume that the pulleys and string are ideal).
 View Solution
View SolutionIn the arrangement shown, the pulleys and the strings are ideal.The acceleration of the block B is
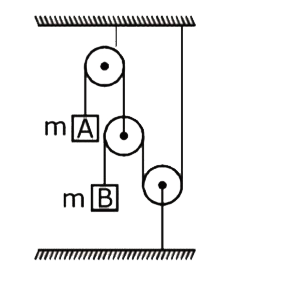 View Solution
View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
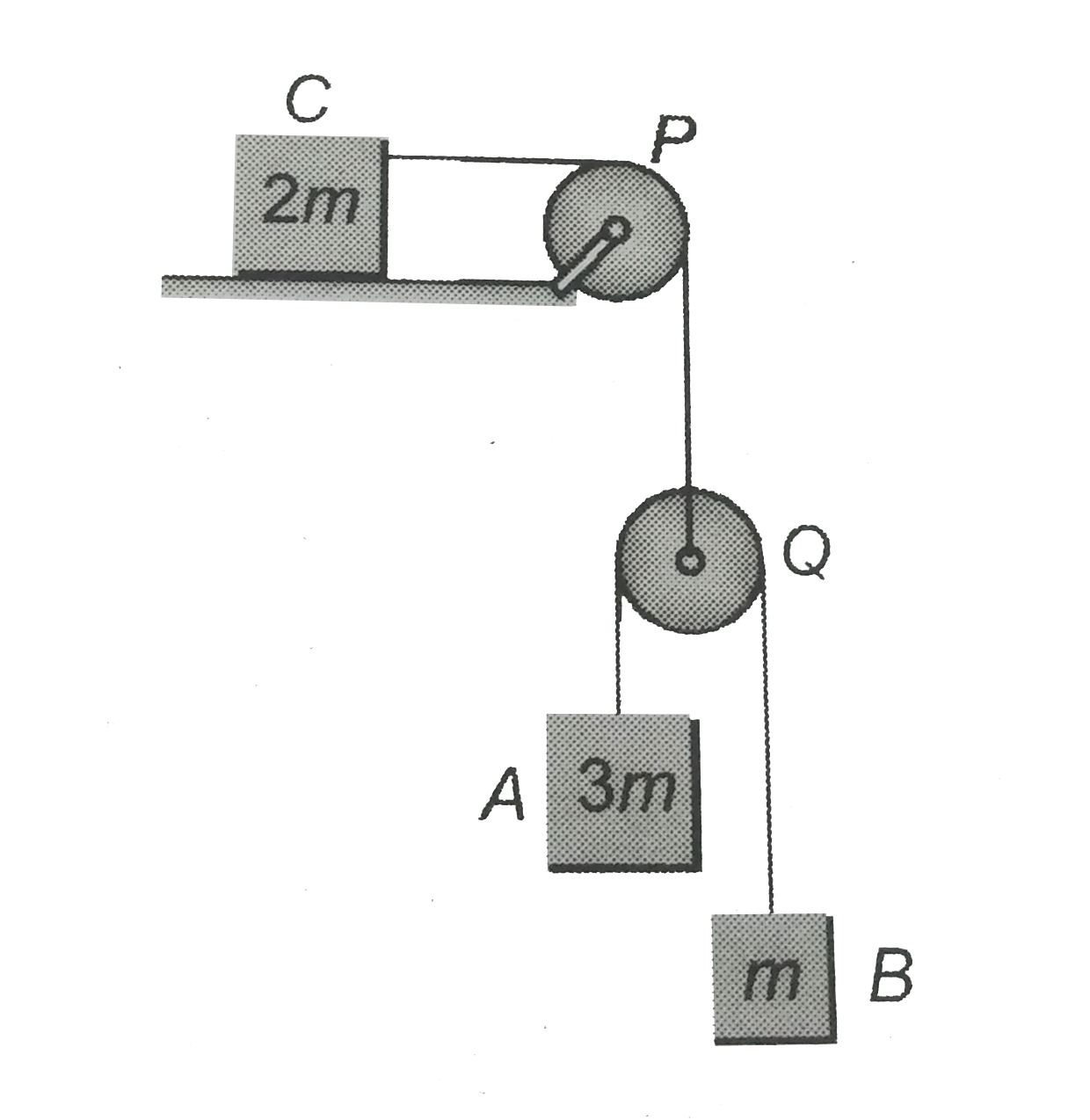 View Solution
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.
 View Solution
View Solution

