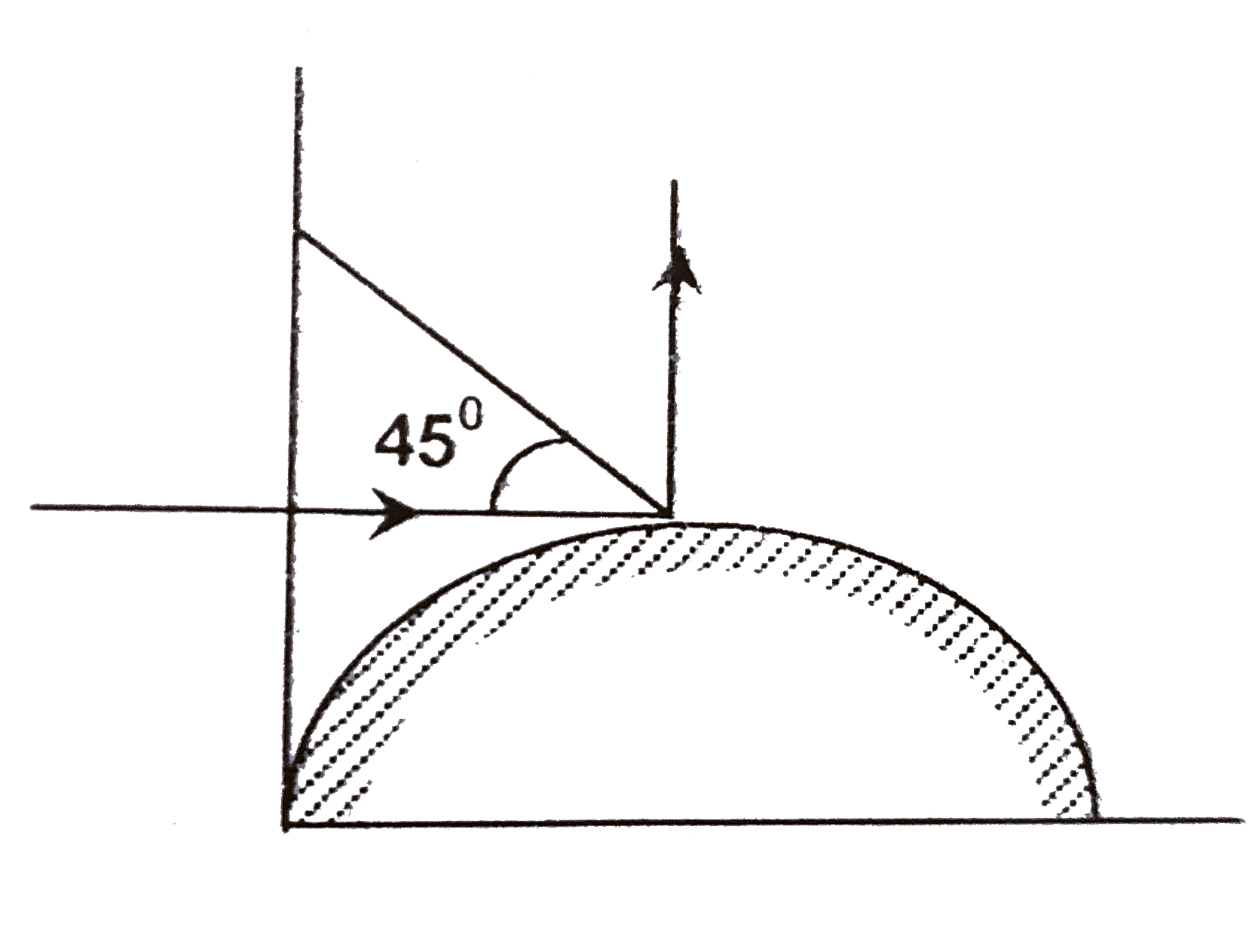
A reflecting surface is represented by the equation $y = \frac{2 L}{π} sin (\frac{π x}{L}), 0 \leq x \leq L$ . A ray traveling horizontal becomes vertical after reflecting. The co-ordinates of the point(s) on which this ray is incident.

$(\frac{L}{4}, \frac{\sqrt{2} L}{π})$

$(\frac{L}{3}, \frac{\sqrt{3} L}{π})$

$(\frac{3 L}{4}, \frac{\sqrt{2} L}{π})$

$(\frac{2 L}{3}, \frac{\sqrt{3} L}{π})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, D

Answer

Step by step video & image solution for A reflecting surface is represented by the equation y=(2L)/pisin((pix)/L),0lexleL. A ray traveling horizontal becomes vertical after reflecting. The co-ordinates of the point(s) on which this ray is incident. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

A reflecting surface is represented by the equation $y = \frac{2 L}{π} sin (\frac{π x}{L}), 0 \leq x \leq L$ . A ray traveling horizontal becomes vertical after reflecting. The co-ordinates of the point(s) on which this ray is incident.

The correct Answer is:B, D

Topper's Solved these Questions

Similar Questions

AAKASH SERIES-GEOMETRICAL OPTICS-LECTURE SHEET (EXERCISE I LEVEL -II (ADVANCED) MORETHAN CORRECT ANSWER TYPE QUESTIONS)

A reflecting surface is represented by the equation y=2Lπsin(πxL),0≤x≤L. A ray traveling horizontal becomes vertical after reflecting. The co-ordinates of the point(s) on which this ray is incident.

The correct Answer is:B, D

Topper's Solved these Questions

Similar Questions

AAKASH SERIES-GEOMETRICAL OPTICS-LECTURE SHEET (EXERCISE I LEVEL -II (ADVANCED) MORETHAN CORRECT ANSWER TYPE QUESTIONS)

A reflecting surface is represented by the equation $y = \frac{2 L}{π} sin (\frac{π x}{L}), 0 \leq x \leq L$ . A ray traveling horizontal becomes vertical after reflecting. The co-ordinates of the point(s) on which this ray is incident.