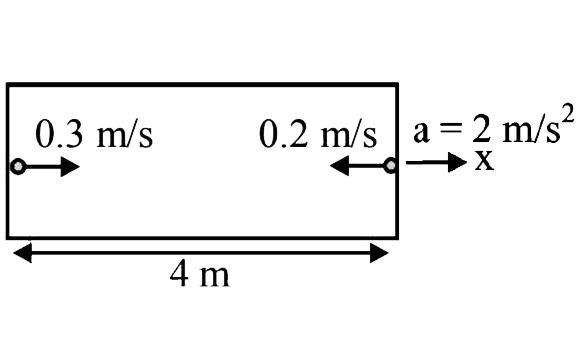
A rocket is moving in a gravity free space with a constant acceleration of 2m/s2 along +x direction (see figure). The length of a chamber inside the rocket is 4m. A ball is thrown from the left end of the chamber in +x direction with a speed of 0.3m/s relative to the rocket . At the same time , another ball is thrown in +x direction with a speed of 0.2m/s drom its right end relative to the rocket . The time in seconds when the two balls hit each other is
The correct Answer is:2
Consider motion of two balls with respect to rocket
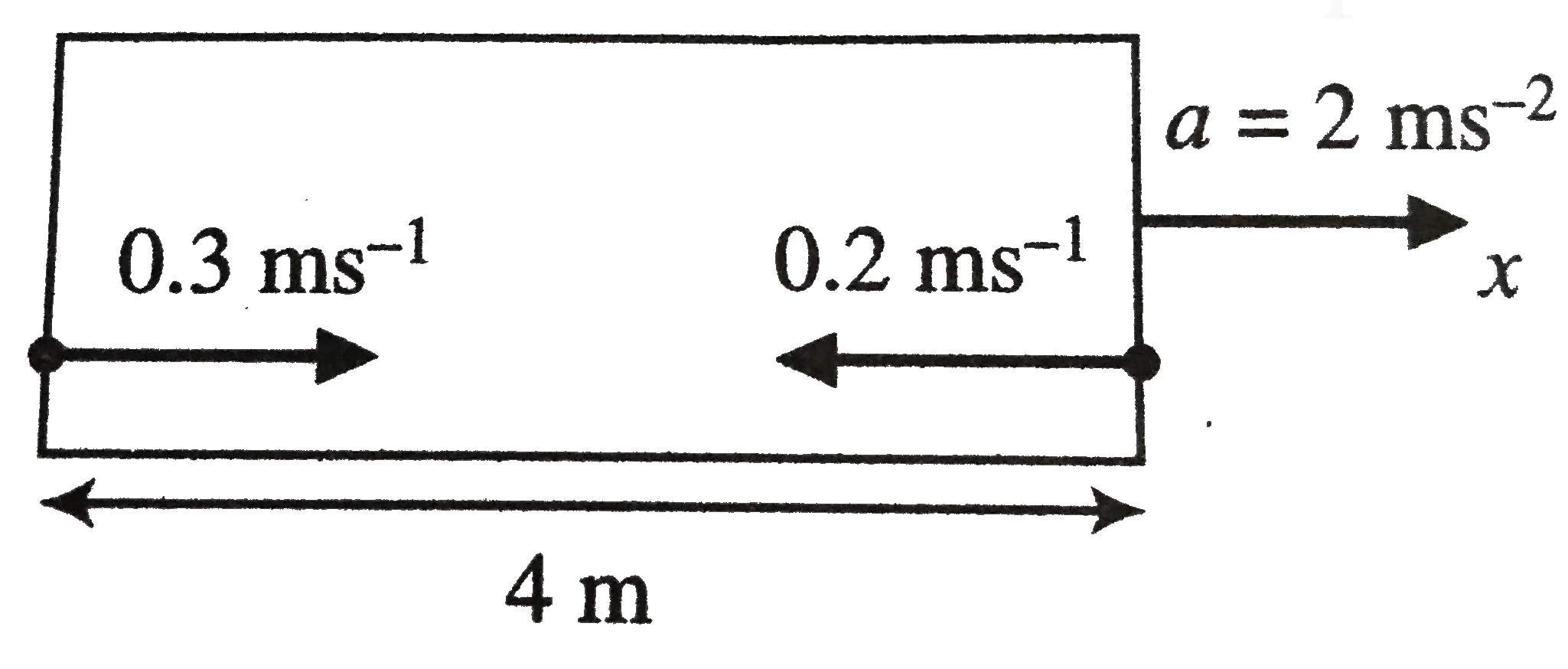
Maximum distance of ball A from left wall
u22a=0.3×0.32×2=0.094≈0.02m
So collision of two balls will take place very near to left wall
For BS=ut+12at2
−4=−0.2t−(12)2t2⇒t2+0.2t−4=0
⇒t=−0.2±√0.04+162=1.9
nearest integer = 2s.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - True or False
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A ball is throuwn with a speed of 20 m//s from top of a buling 150 m high and simultaneously another ball is thrown vertically upward witn a speed of 30 m/s from the foot of the builing . Find the time when both the balls will meet (g=10m/s2)
View SolutionA particle (A) is dropped from a height and another particles (B) is thrown into horizontal direction with speed of 5m/s sec from the same height. The correct statement is
View Solution
Knowledge Check
A ball A is dropped from a building of height 45m. Simultaneously another ball B is thrown up with a speed 40m/s. Calculate the relative speed of the balls as a function of time.
A0B10ms−1C25ms−1D50ms−1A cricket ball is thrown at a speed of 30 m s−1 in a direction 30∘ above the horizontal. The time taken by the ball to return to the same level is
A2 sB3 sC4 sD5 s
A ball is thrown up at a speed of 4.0 m/s. Find the maximum height reached by the ball. Take g=10m/s2.
View SolutionFrom a height of 100 m, a ball is thrown horizontally with an initial speed of 15m/s. How far does it travel horizontally in the first 2 seconds ?
View SolutionA ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. The relative speed of the balls varies with time as
View SolutionA ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
View SolutionA ball A is dropped from a building of height 45m. Simultaneously another ball B is thrown up with a speed 40m/s. Calculate the relative speed of the balls as a function of time.
View SolutionA ball is thrown downwards with a speed of 20ms−1, from the top of a building 150m high and simultaneously another ball is thrown vertically upwards with a speed of 30ms−1 from the foot to the building . Find the time after which both the balls will meet. (g=10 m s^(-2))
 .
.
View Solution
