A shell is fired from a cannon with a speed of 100m/s at an angle 30∘with the vertical (y-direction). At the highest point of its trajectory, the shell explodes into two fragments of masses in the ratio 1:2. The lighter fragment moves vertically upwards with an initial speed of 200m/s. What is the speed of the heavier fragment at the time of explosion?
To solve the problem, we will follow these steps:
Step 1: Determine the initial horizontal and vertical components of the shell's velocity.
The shell is fired at a speed of 100m/s at an angle of 30∘ with the vertical. Therefore, we can find the components of the initial velocity:
- The vertical component uy:
uy=100cos(30∘)=100×√32=100×0.866=86.6m/s
- The horizontal component ux:
ux=100sin(30∘)=100×12=50m/s
Step 2: Analyze the motion at the highest point.
At the highest point of its trajectory, the vertical component of the velocity becomes zero (vy=0). The horizontal component remains ux=50m/s.
Step 3: Apply the conservation of momentum in the vertical direction.
The shell explodes into two fragments with masses in the ratio 1:2. Let the mass of the lighter fragment be m and the heavier fragment be 2m. The lighter fragment moves vertically upwards with a speed of 200m/s.
Using conservation of momentum in the vertical direction:
m⋅200+2m⋅vy=0
Where vy is the speed of the heavier fragment in the vertical direction. Solving for vy:
200m+2mvy=0⟹2mvy=−200m⟹vy=−100m/s
This indicates that the heavier fragment moves downward with a speed of 100m/s.
Step 4: Apply the conservation of momentum in the horizontal direction.
Since the lighter fragment has no horizontal motion after the explosion, we can write:
m⋅0+2m⋅vx=3m⋅ux
Where vx is the horizontal speed of the heavier fragment. Solving for vx:
2mvx=3m⋅50⟹vx=3⋅502=75m/s
Step 5: Calculate the resultant speed of the heavier fragment.
Now, we can find the resultant speed v of the heavier fragment using the Pythagorean theorem:
v=√v2x+v2y=√(75)2+(−100)2=√5625+10000=√15625=125m/s
Final Answer:
The speed of the heavier fragment at the time of explosion is 125m/s.
---
The shell is fired at a speed of 100m/s at an angle of 30∘ with the vertical. Therefore, we can find the components of the initial velocity:
uy=100cos(30∘)=100×√32=100×0.866=86.6m/s
ux=100sin(30∘)=100×12=50m/s
At the highest point of its trajectory, the vertical component of the velocity becomes zero (vy=0). The horizontal component remains ux=50m/s.
The shell explodes into two fragments with masses in the ratio 1:2. Let the mass of the lighter fragment be m and the heavier fragment be 2m. The lighter fragment moves vertically upwards with a speed of 200m/s.
m⋅200+2m⋅vy=0
Where vy is the speed of the heavier fragment in the vertical direction. Solving for vy:
200m+2mvy=0⟹2mvy=−200m⟹vy=−100m/s
This indicates that the heavier fragment moves downward with a speed of 100m/s.
Since the lighter fragment has no horizontal motion after the explosion, we can write:
m⋅0+2m⋅vx=3m⋅ux
Where vx is the horizontal speed of the heavier fragment. Solving for vx:
2mvx=3m⋅50⟹vx=3⋅502=75m/s
Now, we can find the resultant speed v of the heavier fragment using the Pythagorean theorem:
v=√v2x+v2y=√(75)2+(−100)2=√5625+10000=√15625=125m/s
The speed of the heavier fragment at the time of explosion is 125m/s.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.324videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
A shell of mass 20kg at rest explodes into two fragments whose masses are in the ratio 2:3. The smaller fragment moves with a velocity of 6m/s. The kinetic energy of the larger fragment is
View SolutionA shell of mass 20kg at rest explodes into two fragments whose masses are in the ratio 2:3. The smaller fragment moves with a velocity of 6m/s. The kinetic energy of the larger fragment is
View Solution
Knowledge Check
- Question 1 - Select One
1 kg body explodes into three fragements. The ratio of their masses is 1:1:3. The fragments of same mass move perpendicular to each other with speed 30 m/s. The speed of heavier part is
A10√2 m/sB10√2 m/sC20√2 m/sD30√2 m/s
A stationary shell explodes into two fragments, having masses in the ratio of 1:2. The heavier fragment attains a Kinetic energy of 100J. The Kinetic energy released in the explosion is:
View SolutionA shell is projected by a cannon at an angle 30∘ with the vertical for a horizontal range R. It explodes at the highest point of its trajectory. Now match the column I and II.
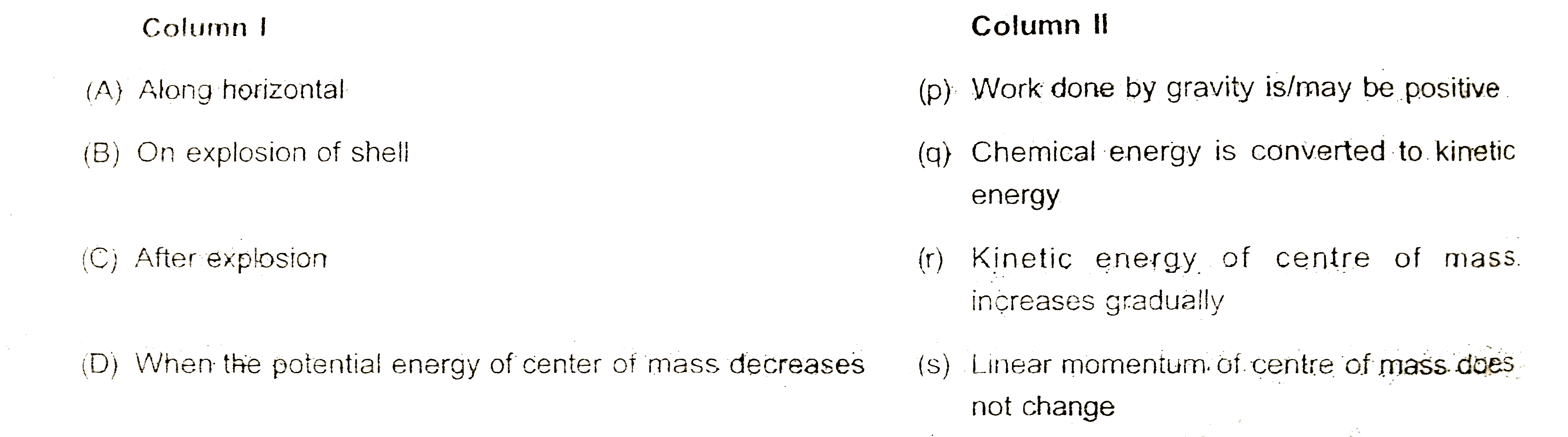 View Solution
View SolutionA shell is fired from a cannon with a velocity V at an angle θ with the horizontal direction. A the highest point i its path, it explodes into two pieces of equal masses. One of the pieces retraces its path to the cannon. The speed of the other piece immediately after the explosion is
View SolutionThe object at rest suddenly explodes into three parts with the mass ratio 2:1:1. The parts of equal masses move at right angles to each other with equal speeds. What is the speed of the third part after the explosion?
View SolutionA projectile is fired with velocity v0 at angle 60∘ with horizontal. At top os its trajectory it explodes into three fragments of equal masses. First fragment retraces the path, second moves vertically upwards with speed 3v02. Speed of the third fragment is
View SolutionA body of mass 1kg initially at rest explodes and breaks into threee fragments of masses in the ratio 1:1:3. The two pieces of equal masses fly off perpendicular to each other with a speed of 30m/s each What is the velocity of heavier fragments ? .
View SolutionA bomb initially at rest at a height of 40 m above the ground suddenly explodes into two identical fragments. One of them starts moving vertically downwards with an initial speed of 10 m/s. If acceleration due to gravity is 10 m/s2, the separation between the fragments, 2 seconds after the explosion is
View Solution

