A simple harmonic oscillator at the point x=0 genrates a wave on a rope. The oscillator operates at a frequency of 40.0 Hz and with an amplitude of 3.00 cm. the rope has a linear mass density of 50.0g/m and is strectches with a tension of 5.00 N. (a) determine the speed of the wave. (b) find the wavelength. (c ) write the wave function y(x,t) for the wave, Assume that the oscillator has its maximum upward displacement at time t=0. (d) find the maximum transverse acceleration at time t=0. (d) find the maximum transverse of points on the rope. (e) in the discussion of transverse waves in this chapter, the force of gravity was ignored. is that a reasonable assumption for this wave? explain.
(a). V=√F/μ=√(5.00N)/(0.0500kg/m)=10.0m/s
(b). Λ=c/f=)10.0m/s)/(40.0Hz)=0.250m
(c ) y(x,t)=Acos(kx−ωt)(note:y(0.0)=A, as specified.)<br>k=2pi//lambda=8pi rad//m, omega=2pif=80.0pi rad//s<br>y(x,t)=(300 cm)cos[pi(8.00 rad//m)x-(80.0pi rad//s)t]<br>(d).v_(y)=+Aomegasin(kx-omegat) and a_(y)=-Aomega^(2)cos(kx-omegat)<br>a_(y,max)=Aomega^(2)=A(2pif)^(2)=1890 m//s^(2)<br>(e)a_(y,max)isμchlar≥rthang,sog can be ignored.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Subjective16videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct62videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.19videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Determine the wave speed of a wave that has a wavelength of 4 mm and a frequency of 3Hz.
View SolutionThe streight shown in figure is driven at a frequency of 5.00Hz. The amplitude of the motion is 12.0cm, and the wave speed is 20.0m/s. Furthmore, the wave is such that y=0 and t=0. Determine (a) the angular frequency and (b) wave number for this wave (c) Write an expression for the wave funcation. Calculate. (d) the maximum transverse speed and (e) the maximum transverse acceleration of a point on the string.
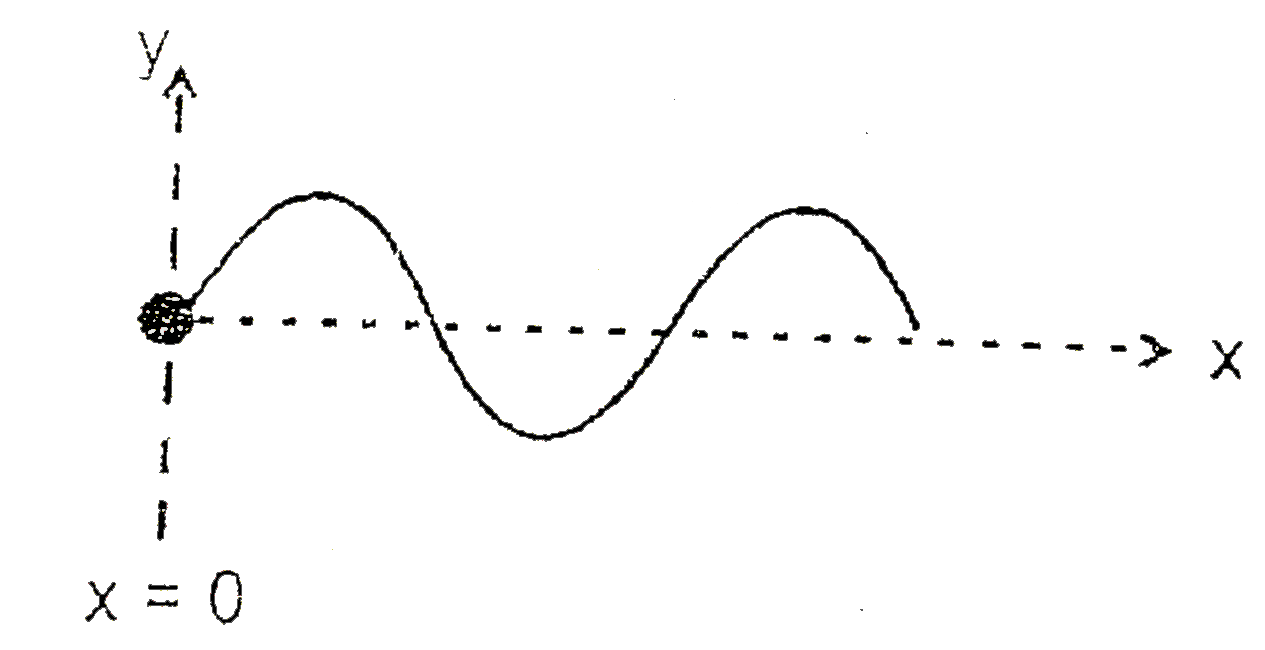 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A string of linear density 0.2 kg/m is stretched with a force of 500 N. A transverse wave of length 4.0 m in set up along it. The speed of wave is
A50 m/sB75 m/sC150 m/sD200 m/s - Question 2 - Select One
A string of linear density 0.2kg/m is stretched with a force of 500 N. If a transverse wave of wavelength 4m and amplitude (1/π) metre is travelling along it, then the speed of the wave will be
A50m/sB62.5m/sC12.5m/sD250m/s
The streight shown in figure is driven at a frequency of 5.00Hz. The amplitude of the motion is 12.0cm, and the wave speed is 20.0m/s. Furthmore, the wave is such that y=0 and t=0. Determine (a) the angular frequency and (b) wave number for this wave (c) Write an expression for the wave funcation. Calculate. (d) the maximum transverse speed and (e) the maximum transverse acceleration of a point on the string.
 View Solution
View SolutionA 200Hz wave with amplitude 1mm travels on a long string of linear mass density 6g/m keep under a tension of 60N.
(a) Find the average power transmitted across a given point on the string.
(b) Find the total energy associated with the wave in a 2.0m long portion of the string.View SolutionA string fixed at both ends is 8.40m long and has a mass of 0.120kg. It is subjected to a tension of 96.0N and set oscillating. (a) What is the speed of the waves on the string? (b) What is the longest possible wavelength for a standing wave ? (c) Give the frequency of the wave.
View SolutionA string fixed at both ends is 7.50 m long and has a mass of 0.120 kg. It is subjected to a tension of 96.0 N and set oscillating (a) What is the speed of the waves on the string? (b) What is thc longest possible wavelength for a standing wave? (c) Give the frequency of that wave.
View SolutionTransverse waves travel with a speed of 20.0m/sin a string under a tension of 6.00 N. what tension is requared for a wave speed of 30.0m/s in the same string?
View SolutionA sinusoidal wave on a string is described by the wave function where x and y are in metres and t is in seconds. The mass per unit length of this string is 12.0g/m. Determine (a) the speed of the wave, (b) the wavelength, (c ) the frequency and (d) the power transmitted to the wave.
View Solution

