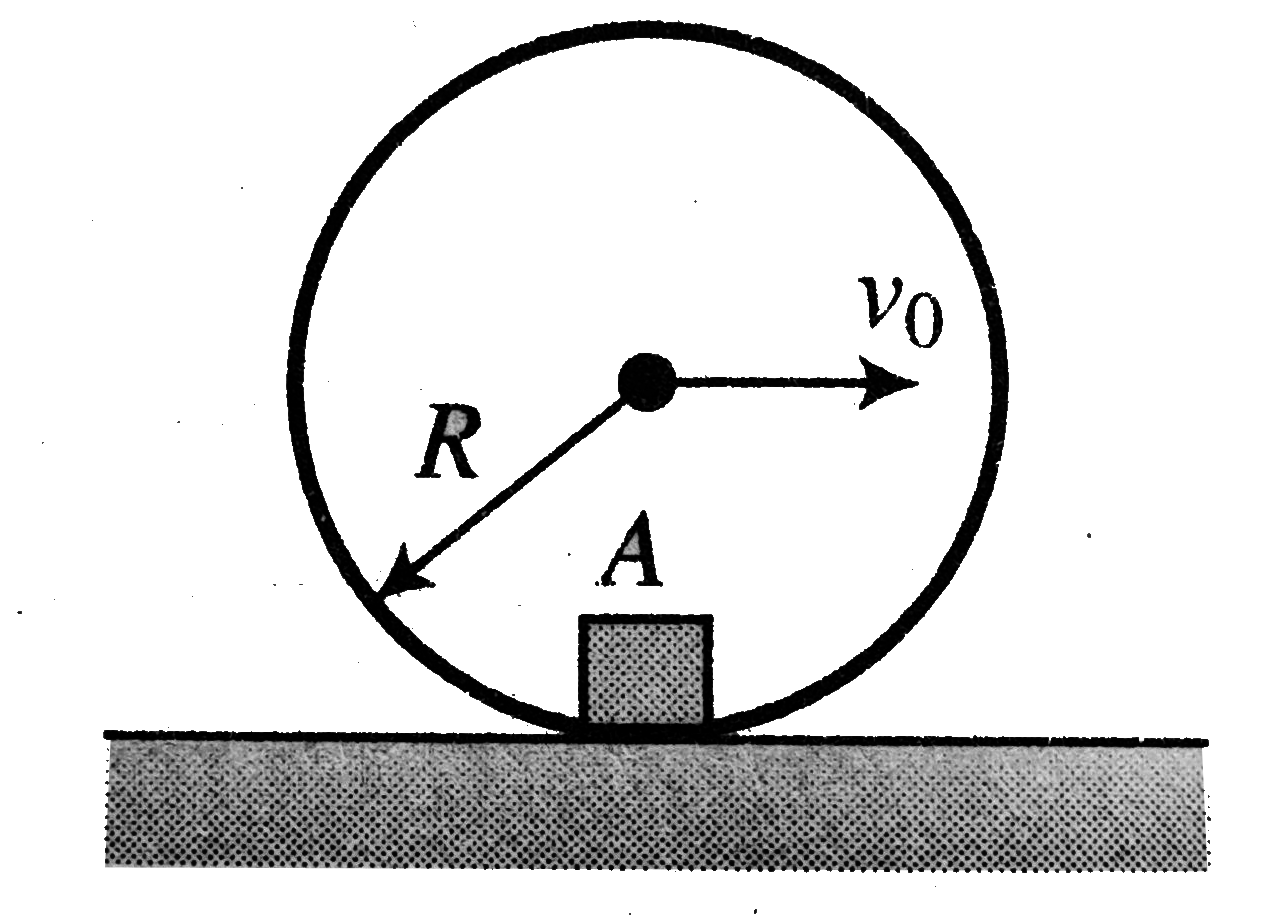
A small body is fixed to the inside of a thin rigid hoop of radius and mass equal to that of the body . The hoop rolls without slipping over a horizontal plane, at the moments when the body gets into the lower position, the centre of the hoop moves with velocity . At what values of will the hoop move without bouncing?
The correct Answer is:
One the hoop, the grond is giving a normal force . Again the attached mass is also giving a normal force . Now value of is changing as the attached body is changing its position. Value of is minimum when the attached body is at the highest position in its circular motion. but this minimum value of should also the greater than zero to prevent the hoop from bouncing.
Now consider of the attached body
.i
[where velocity of cenntre of mass of the hoop at tis moment. Again velocity of the body at its moment with respect to the hooop centre of mass ]
For the hoop
.....ii
From i and ii
..........iii
........iv
Now conserving energying the reference rame of the ground:
Putting and
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A uniform sphere of mass m and radius r rolls without sliding over a horizontal plane, rotating ahout a horizontal axle OA. In the process, the centre of the sphere moves with a veocity v along a circle of radius R. Find the kinetic energy of the sphere.
View Solution
A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration atView SolutionA uniform solid cylinder of radius 'R' has a circular cut of radius R2 from the edge, Its mass is M. It is rolling wihtout slipping on a rough horizontal floor. When the cut part is at lowest position, centre of the disc is moving with horizontal velocity v. Choose the alternative:
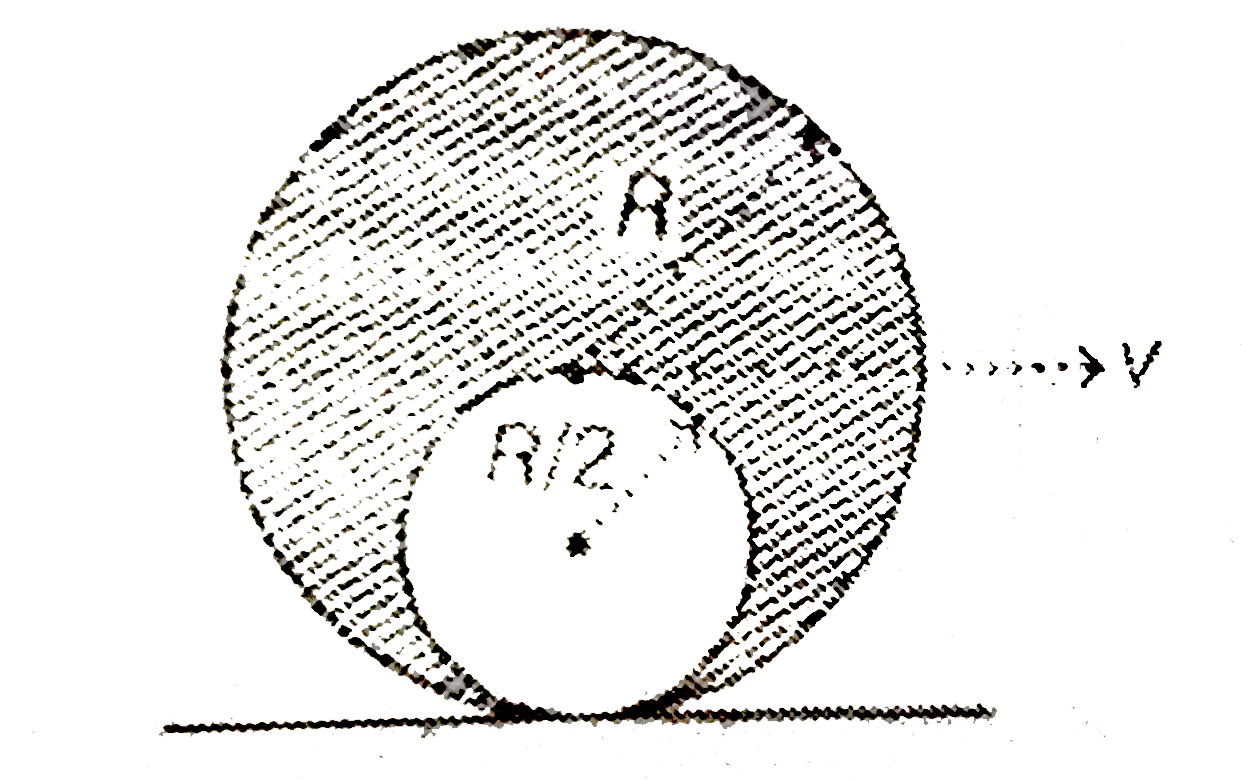 View Solution
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View SolutionA body of mass M moving with velocity V explodes into two equal parts. If one comes to rest and the other body moves with velocity v, what would be the value of v ?
View SolutionA round uniform body of radius R, mass M and moment of inertia 'I' rolls down (without slipping) and inclined plane making an angle θ with the horizontal. Then its acceleration is.
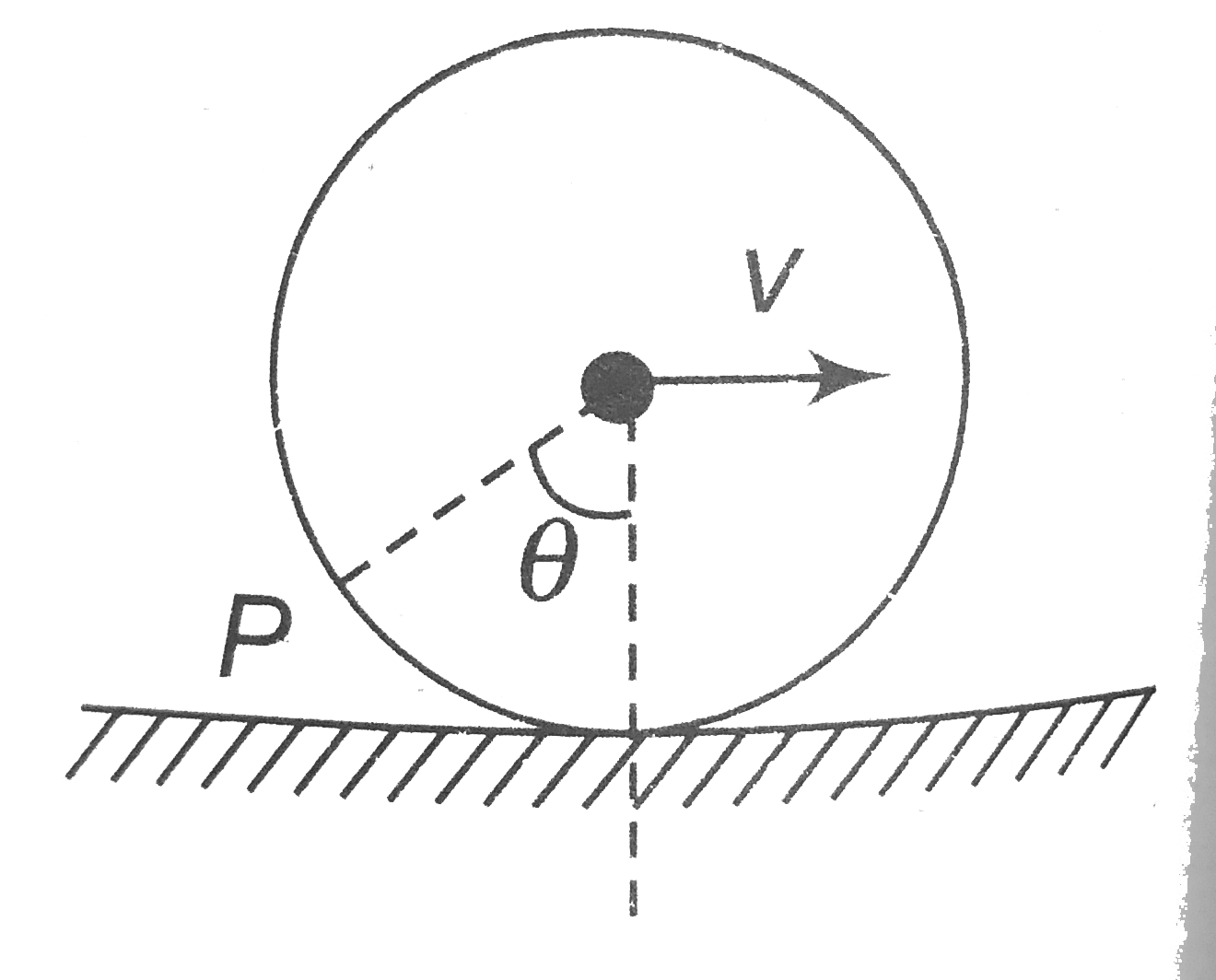
View SolutionA hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
 View Solution
View SolutionA uniform thin spherical shell of mass m and radius R rolls down without slipping over an inclined plane of angle θ with the horizontal. The ratio of rotational kinetic energy to the total kinetic energy of the shell will be
View SolutionA wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is
 View Solution
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View Solution
