A small body of mass m can slide without friction along a through bent which is in the form of a semi-circular arc of radius R. At what height h will the body be at rest with respect to the trough, if the trough rotates with uniform angular velocity ω about a vertical axis:

R
R−2gω2
R+2gω2
R−gω2
The correct Answer is:d
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-273videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-349videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Example95videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-334videos
DESCRIPTION OF MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
Similar Questions
A small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the surface of hemisphere?
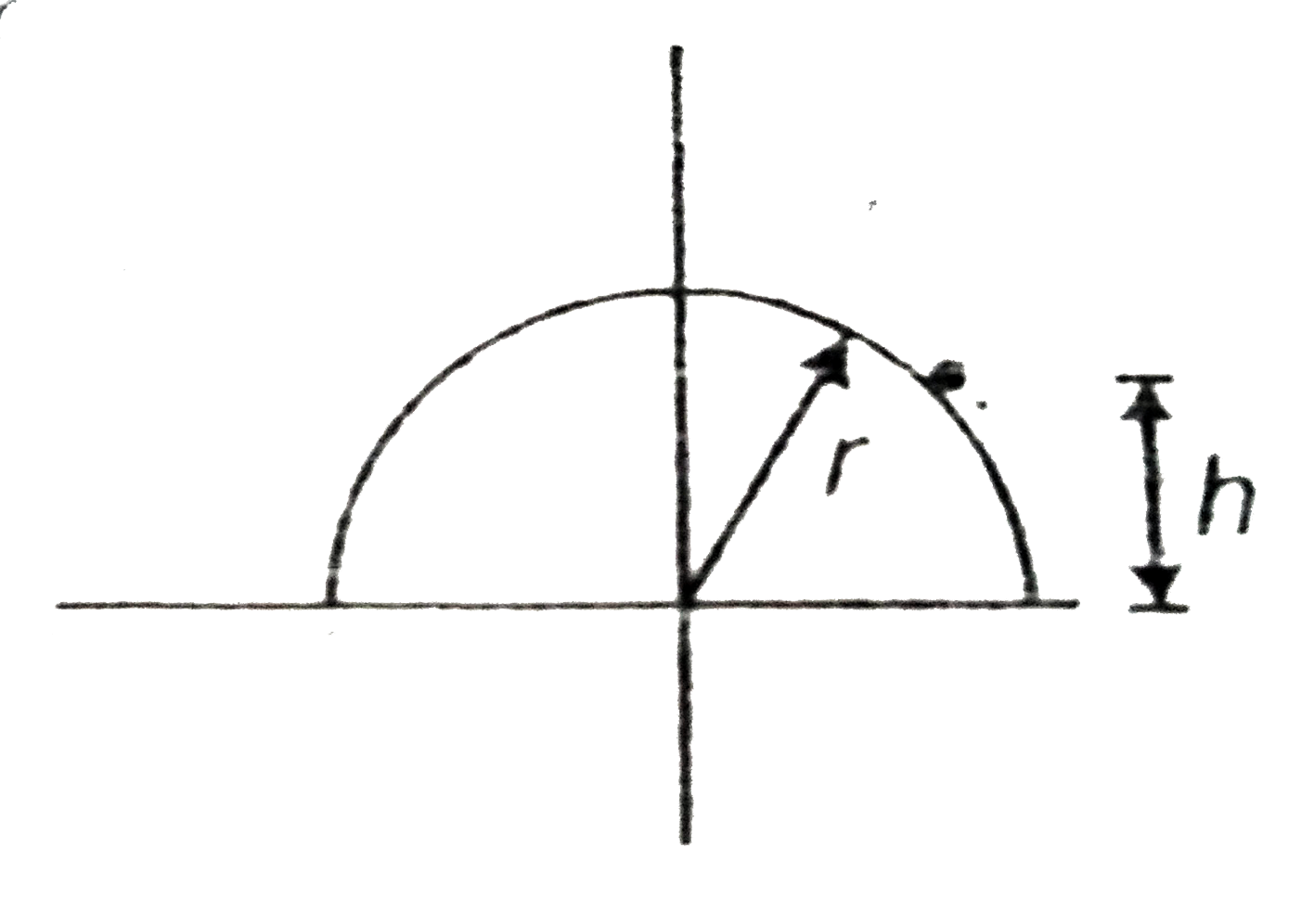 View Solution
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the centre of hemisphere?
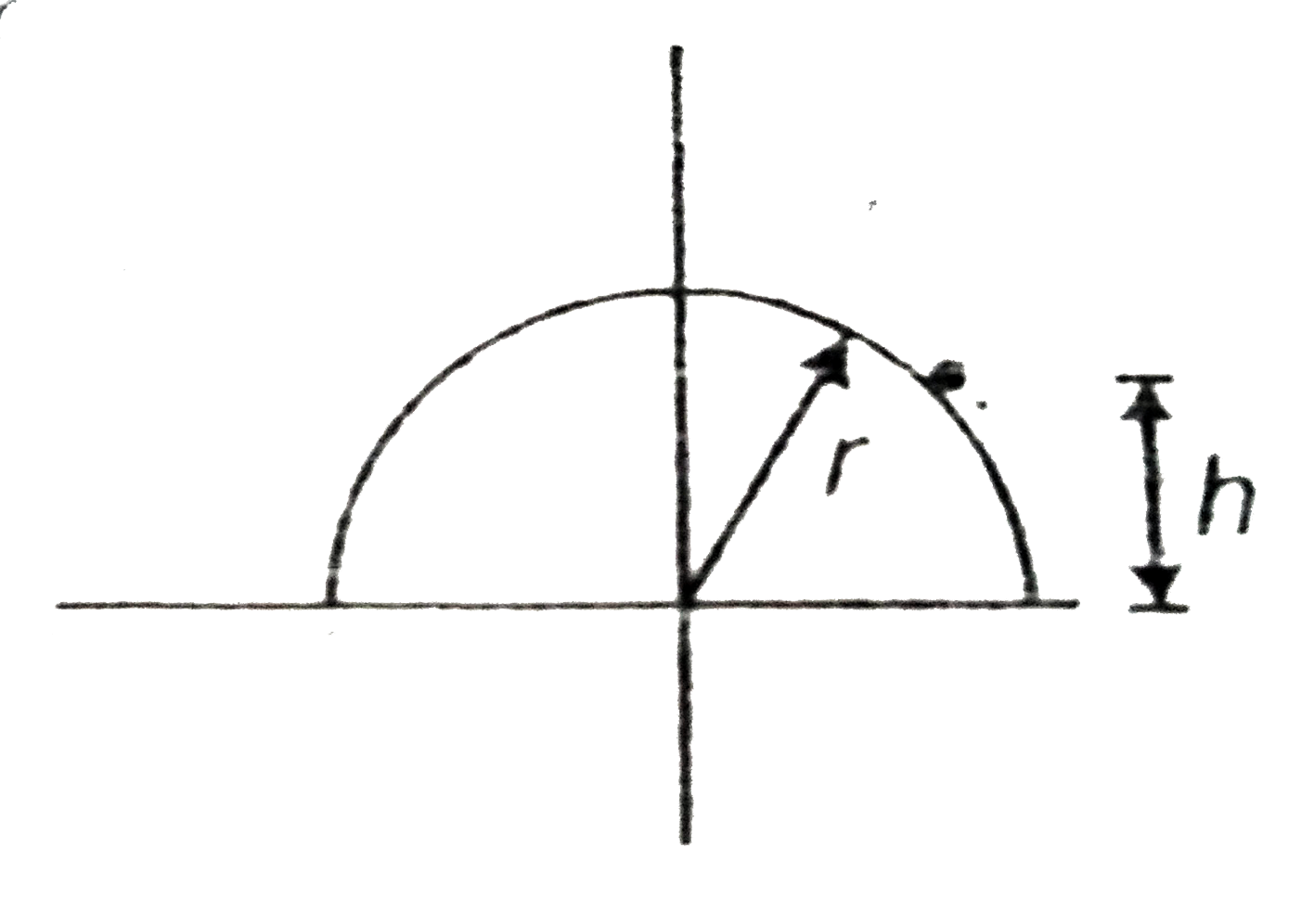 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
Akinetic energy of the bodyBtwice the kinetic energy of the bodyCangular momentum of the bodyDtwice the angular momentum of the body - Question 2 - Select One
A rigid body of mass m rotates about an axis passing through its centre. If the angular velocity of the body is unity, the moment of inertia of the body will be equal to
Akinetic energy of the bodyBtwice the kinetic energy of the bodyCangular momentum of the bodyDtwice the angular momentum of the body - Question 3 - Select One
A thin circular ring of mass m and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass M are attached gently to the opposite ends of a diameter of the ring. The ring now rotates with an angular velocity ω'=
Aω(m+2M)mBω(m−2M)(m+2M)Cωm(m+M)Dωm(m+2M)
A horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.View SolutionA horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R(figure). The system is set in rotation with a constant angular velocity ω about a vertical axis OO′. Find the angle θ corresponding to the steady position of the sleeve.
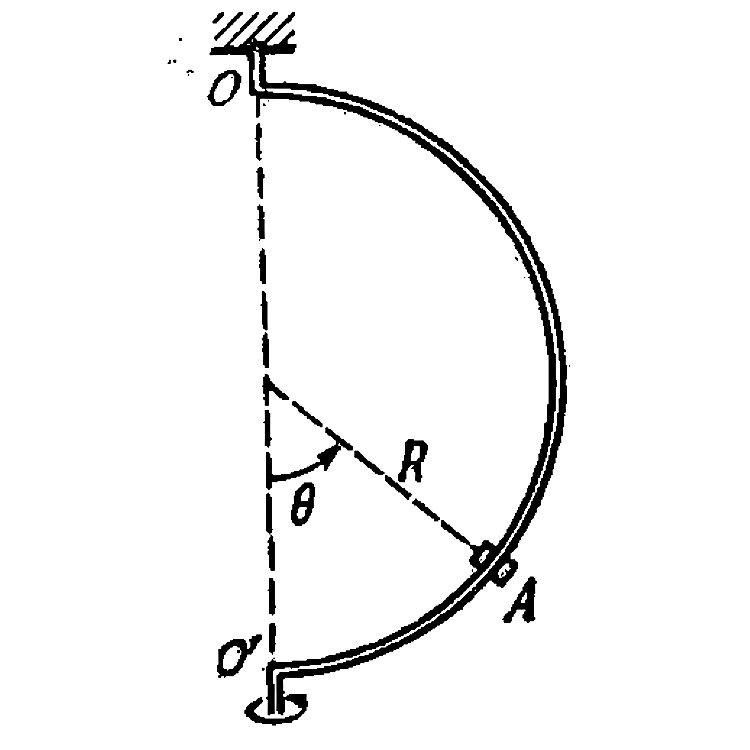 View Solution
View Solution

