A small bucket of mass M is attached to a long inextensible cord of length L. The bucket is released from rest when the cord is in a horizontal position. In its lowest position the bucket scoops up m of water, what is the height of the swing above the lowest position?
The correct Answer is:l
Let the bucket of the mass M reach the lowest position with a speed v. As it scoops up a water of mass m, at the lowest position, its peed decreases to v,. The speed of the bucket just after scooping of water is given by conserving momentum of the system just before and after scooping of water we obtain
Mv=⇒(M+m)v'
⇒v'=MvM+m.....i
Conservation of energy of the bucket between A and B (just before scooping) yields, (12)mv2−mgl=0
⇒v=√2gl......ii

Conservation of energy of the bucket + water between B and C after the scooping) of water, yields
12mv'2−mgh=0⇒h=v'22g.............iii
By using i, ii and iii we obtain h=(MM+m)2l
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Single Correct
141 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.3
24 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
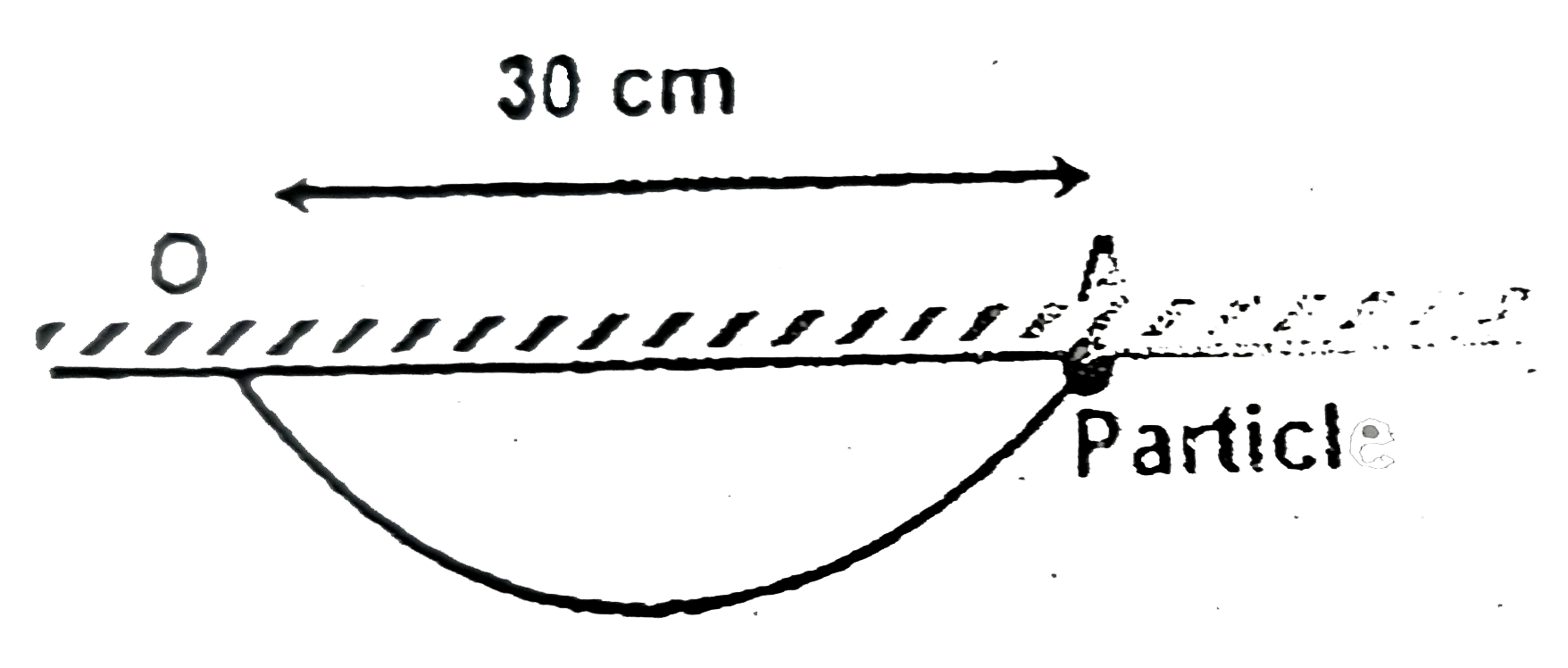
A small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
View SolutionA particle of mass m attached with a massless spring natural length l and stiffness k is released from rest from the horizontal position of the relaxed spring. When the particle passes through its lowest point, the maximum length of the spring becomes 2l. Find the:
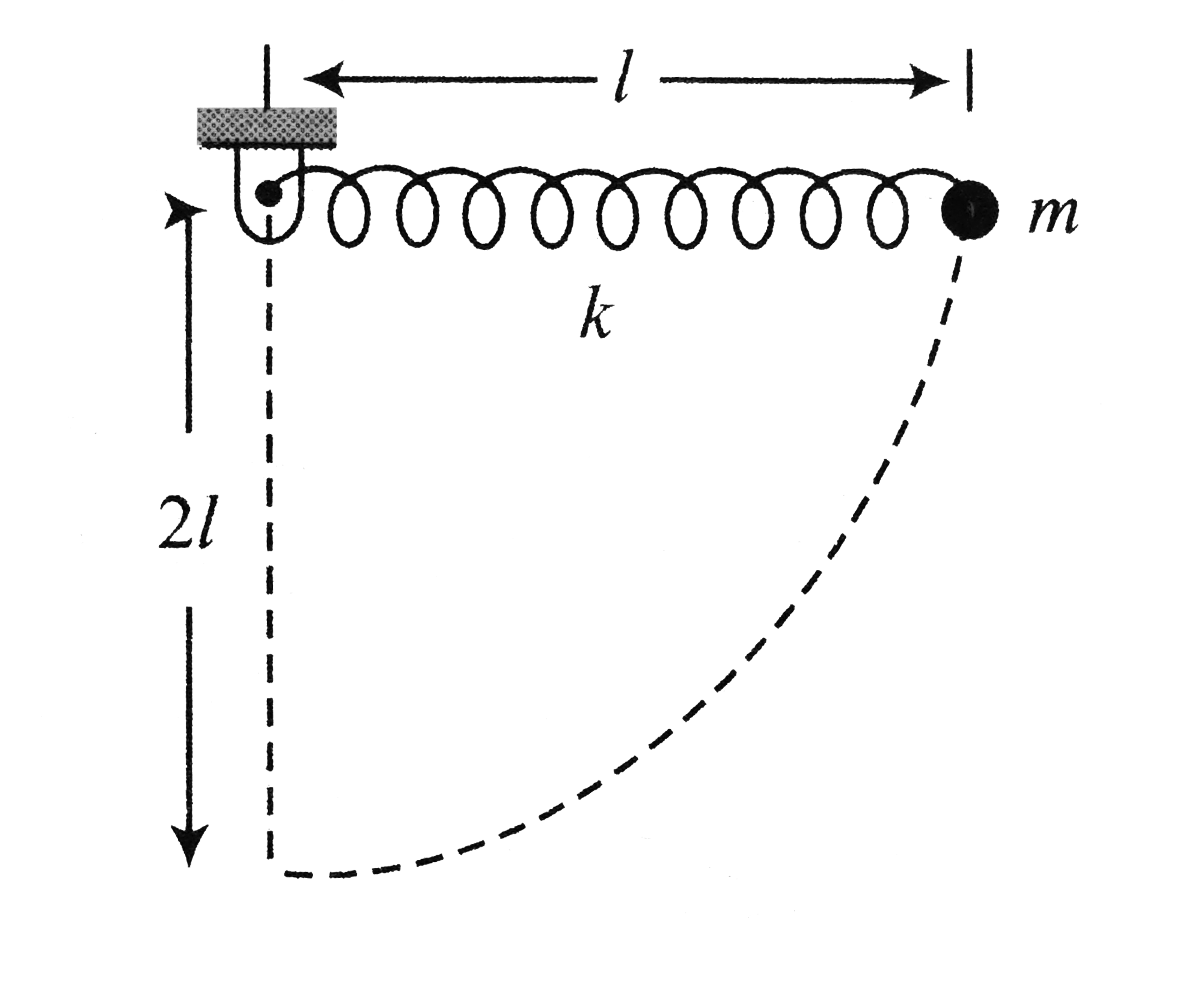
a. speed of the particle at its lowest point.
b. acceleration of the particle at its lowest position.
View Solution
Knowledge Check
A small bucket of mass M kg is attached to a lone inextensible cord of length L m. The bucket is released from rest when the cord is in a horizontal position. At its lowest position, the bucket scoops up m kg of water and swings up to a height h. The height h in meter is :-
A(MM+m)2LB(MM+m)LC(M+mM)2LD(M+mM)LA block of mass 2m is attached to a string of length L=5m. The block is released when the string is horizontal , it picks up a particle of 2m kept at rest at the lowest point. The maximum height attached by the combined mass is
A1mB1.25mC1.5mD2.0mA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
A√glB√3glC√2glD√5gl
The string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionA partical of mass m attached with a massless spring of natural length l and stiffness constant k is releaased from rest from the horizontal positon of the relaxed spring.

When the particle passes through its lowest point, the maximum length of the spring bocomes 2l find the
(A) Speed of the particle at its lowest point
(B) Acceleration of the particle at its lowest position.
View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View SolutionA bob hangs from a rigid support by an inextensible string of length l. If it is displaced through a distance l (from the lowest position) keeping the string straight and then released. The speed of the bob at the lowest position is

View SolutionA pendulum is released from rest from horizontal position as shown. The tangential acceleration when the pendulum reacheda t lowest when the pendulum reached at lowest position on its path is

View Solution
