A small cart A starts moving on a horizontal surface, assumed to be x-y plane along a straight line parallel to x-axis (see figure) with a constant acceleration of 4m/s2. Initially it is located on the positive y-axis at a distance 9 m from origin. At the instant the cart starts moving, a ball is rolled along the surface from the origin in a direction making an angle 45° with the x-axis. The ball moves without friction at a constant velocity and hits the cart.
(a) Describe the path of the ball in a reference frame attached to the cart.
(b) Find the speed of the ball.
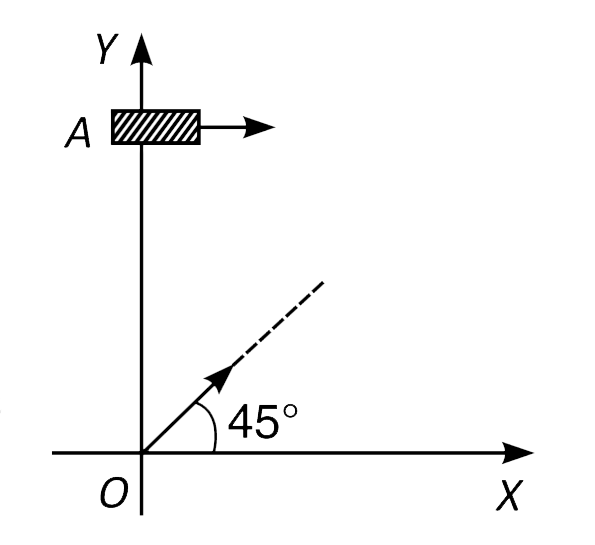
The correct Answer is:(a) Parabolic path (b) 6m/s
Step by step video, text & image solution for A small cart A starts moving on a horizontal surface, assumed to be x-y plane along a straight line parallel to x-axis (see figure) with a constant acceleration of 4 m//s^(2). Initially it is located on the positive y-axis at a distance 9 m from origin. At the instant the cart starts moving, a ball is rolled along the surface from the origin in a direction making an angle 45° with the x-axis. The ball moves without friction at a constant velocity and hits the cart. (a) Describe the path of the ball in a reference frame attached to the cart. (b) Find the speed of the ball. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 258videos
KINEMATICS
- BOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 333videos
KINEMATICS
- BOOK - ARIHANTCHAPTER - HEAT TRANSFEREXERCISE - Heat Transfer45videos
HEAT TRANSFER
- BOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 34videos
KINETIC THEORY OF GASES
Similar Questions
On a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−aξs( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x−aξs , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x−aξsandithitsthetrol≤y.<br>(a)Themotionoftheballisobservedomtheameofthetrol≤y.Calca––tethe∠thetamadebythevelocity→−−→roftheballwiththe x-axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(4).
 View Solution
View SolutionA body starts from the origin with an acceleration of 6ms−1 along the x - axis and 8ms−1 along the y - axis. Find its distance from the origin after 4s.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
Adecreases with timeBincreases with timeCremains constantDis zero - Question 2 - Select One
A body starts from rest from the origin with an acceleration of 3m/s(2) along the x-axis and 4m/s2 along the y-axis. Its distance from the origin after 2s will be
A5mB10mC15mD20m - Question 3 - Select One
A body starts from rest from the origin with an acceleration of 6m/s2 along the x-axis and 8m/s2 along the y-axis. Its distance from the origin after 4 seconds will be
A56 mB64mC80 mD128m
A straight line makes an angle 120 with positive direction of x-axis measured in anti clock direction and makes positive intercept on y-axis and the line is at a distance of 5 units from origin then its equation is
View SolutionA particle starts from the origin with a velocity of 2 cm/s and moves along a straight line. If the acceleration of the particle at a distance x cm from the origin be (2x−32)cms2, find the velocity of the particle at a distance 7 cm from the origin.
View SolutionA body starts from rest from the origin with an acceleration of 6m/s2 along x axis and 8m/s2 along y axis.The distance from origin after 4 seconds will be
View SolutionAn object starts from rest at the origin and moves along the x axis with a constant acceleration of 4m/s2. Its average velocity as it goes from x=2 m to x=8 m is :
View SolutionA straight line makes an angle of 135∘ with the X-axis and cuts Y-axis at a distance -5 from the origin. The equation of the line is
View Solution

