A small fish 0.4 m below the surface of a lake is viewed through a simple converging lens of focal length 3 m. The lens is kept at 0.2 m above the water surface such that fish lies on the optical axis of the lens. The image of the fish seen by observer will be at (μwater=43)

A distance of 0.2m from the water surface
A distance of 0.6m from the water surface
A distance of 0.3m from the water surface
The same location of fish
The correct Answer is:D
Step by step video & image solution for A small fish 0.4 m below the surface of a lake is viewed through a simple converging lens of focal length 3 m. The lens is kept at 0.2 m above the water surface such that fish lies on the optical axis of the lens. The image of the fish seen by observer will be at (mu_("water")=(4)/(3)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERICSE-III (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS ))
10 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERICSE-III (LEVEL-II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ))
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERICSE-II (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS))
5 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
A small fish 0.4 m below the surface of a lake is viewed through a simple converging lens of focal length 3 m.the lens is kep at 0.2 m above the water surface such that the fish lies on the optical axis of the lens. Find the image of the fish seen by the observed. (μwater=43)
View SolutionA stationary observer O looking at a fish F in water (μw=4/3) through a converging lens of focal length 90.0cm . The lens is allowed to fall frelly from a height 62.0cm with its axis vertical. The fish and the observer are on the principal axis of the lens. The fish moves up with constant velocity 100cm/s. Initially it was at depth of 44.0cm . Find the velocity (in cm//s) with which the fish appears to move with respect to lens to the observer at t=0.2s. (take g=10m/s2)
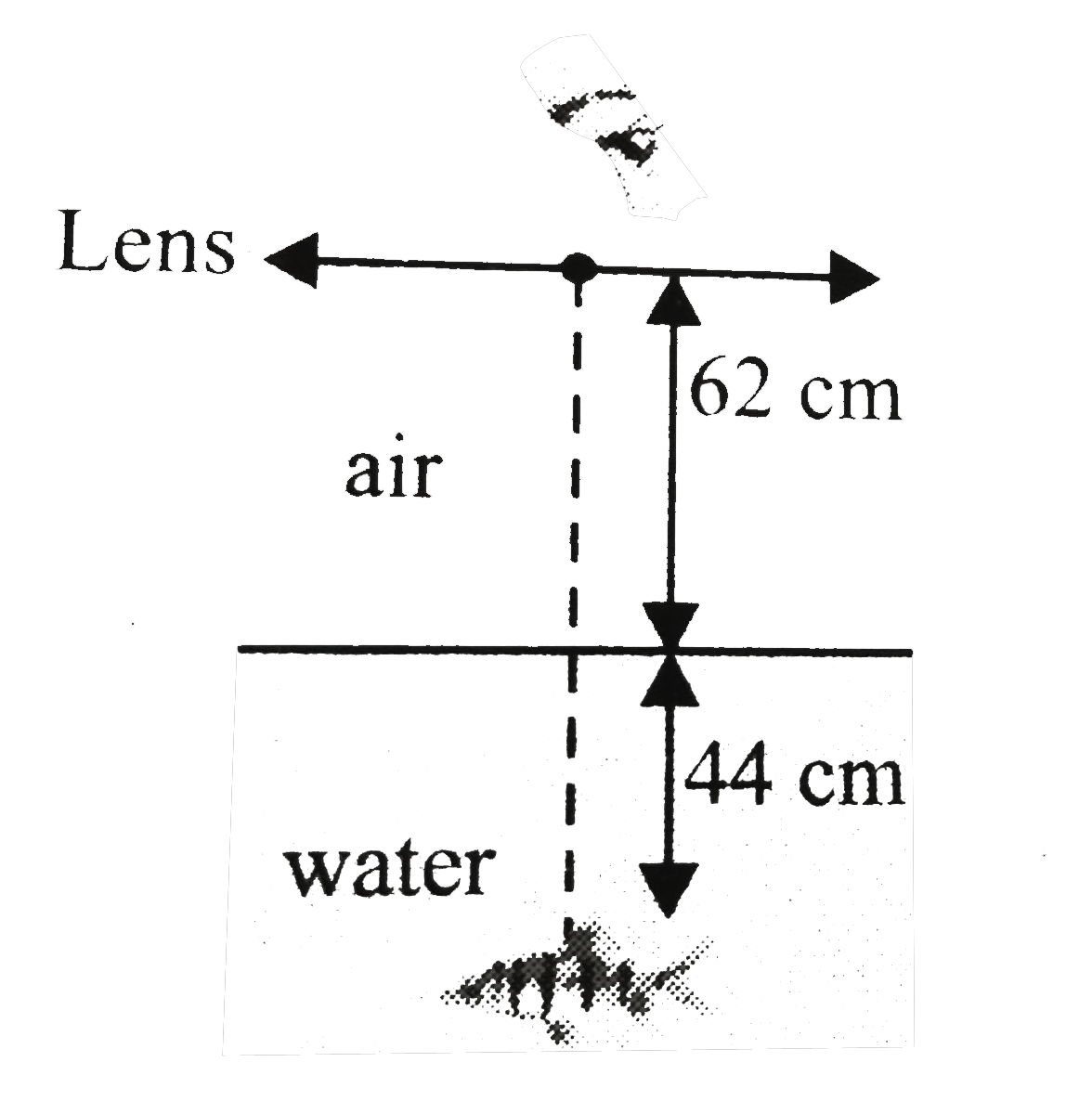
View Solution
Knowledge Check
A convex lens of focal legnth 0.2m and made of glass (μ=1.50) is immersed in water (μ=1.33). Find the change in the focal length of the lens.
A5.8mB0.58cmC0.58mD5.8cmA convergent beam of light passes through a diverging lens of focal length 0.2m and comes to focus at a distance of 0.3m behind the lens. Find the position of the point at which the beam would converge in the absence of the lens.
A0.12mB0.6mC0.3mD0.15m
A converging lens has a focal length of 0.12 m. To get an image of unit magnification the object should be placed at what distance from the converging lens ?
View SolutionAn object is at a distance of 20 m form a convex lens of focal length 0.3m The lens forms an image of the object moves away form the lens at a speed of 5m/s the speed and direction of the image will be :
View SolutionA thin plano - convex lens acts like a concave mirror of focal length 0.2 m, when silvered on its plane surface. The refractive index of the material of the lens is 1.5. The radius of curvature of the convex surface of the lens will be
View SolutionA fish in a lake (refractive index 4/3 for water ) is viewed through a convex lens. From water surface, the lens is placed in air at half of the distance of the fish from the water surface, so that the image is formed at the fish itself. The focal length of the lens is how many times the depth of fish in water?
View SolutionFind the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionA fish lies at the bottom of a 4m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4/3 . Then the distance between
View Solution
