A smooth vertical tube having two different cross sections is open from both the ends but closed by two sliding pistions as shown in Fig. and tied with an inextensible string. One mole of an ideal gas is enclosed between the piston The difference in cross-sectional areas of the two pistons is given ΔS. The masses of piston are m1 and m2 for larger and smaller one, respectively. Find the temperature by which tube is raised so that the pistons will be displaced by a distance l. Take atmospheric pressure equal to P0

If initial pressure of gas is P and let S1 and S2 be the cross-sectional area of the larger and the smaller piston, respectivley, then for equilibrium of the two piston, we have
For larger piston
P0S1m1g+T=PS1 (if T is the tension in string) (i)
For smaller piston
PS2+m2g−(T)+P0S2 (ii)
Adding Eqs. (i) adn (ii), we get
P0(S1−S2)+m1g+m2g=P(S1−S2)+m1g+m2g=P(S1−S2)
or P0(m1+m2ΔS)g=P (iii)
In gas temperature is increased fromm T1 to T2, the volume of gas increase from V to V+lΔS as l is the displacement of pistons, them gas law we must have
PV=RT1 (for initial state) (iv)
P(V+lΔS)=RT2 (for final state) (v)
According to Eq. (iii), we find the pressure of the gas does not change, as does not depend on temperature.
From Eqs. (iv) and (v), if we subtract the these equation, we get
PlΔS=R(T2−T1)
or T2−T1=PlΔSR
=(P0+(m1+m2)ΔSg)lΔSR
[P0ΔS+(m1+m2)g]1R
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.1
20 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.2
28 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
The water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionAn incompressible liquid of density ρ is enclosed with two frictionless pistons one of cross-sectional area A and the other of 4 A. When the narrow piston moves out by a distance.
View Solution2 moles of a diatomic gas are enclosed in a cylinder piston arrangment. The area of cross section and mass of the piston are 1cm2 and 1 kg respectively. A heater is supplying heat to the gas very slowly. Find heat supplied (in joule) by the heater is the piston moves through a distance of 10 cm.
 .
.
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
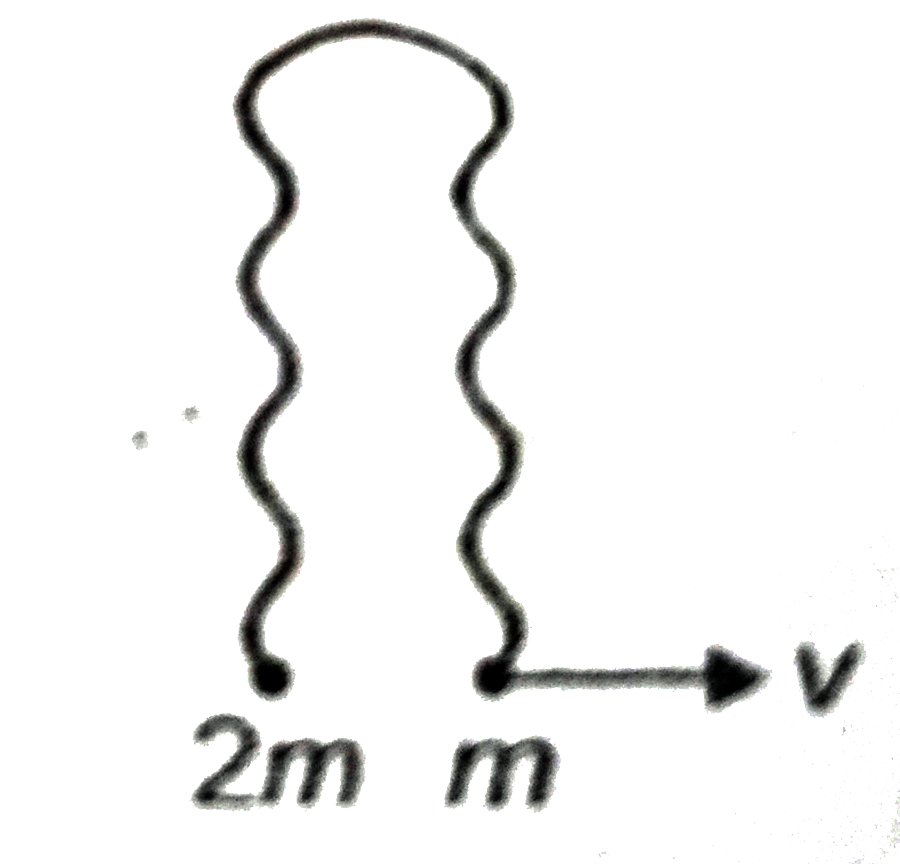
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.

View SolutionWhen a pressure measuring device is immersed in a liquid, a restoring force of 2 N is exerted by the spring. If the area of cross-section of the pistion is 10 cm2, what pressure does the fluid exert on the piston?
View SolutionTwo strings of copper are stretched to the same tension. If their cross-section area are in the ratio 1 : 4 , then the respective wave velocities will be
View SolutionIn the figure, the cross-sectional area of the smaller tube is a and that of the larger tube is 2a. A block of mass m is kept in the smaller tube having the base area that of the tube. The difference between water levels of the two tubes is

View SolutionIn the figure, the cross-sectional area of the smaller tube is a and that of the larger tube is 2a. A block of mass m is kept in the smaller tube having the base area that of the tube. The difference between water levels of the two tubes is

View SolutionA horizontal cylinder has two sections of unequal cross-section, in which two pistons can move freely. The pistons are joined by a string. Some gas is trapped between the pistons . Spring is massless and in natural length. If this gas is heated, the spring will
_PHY_E06_357_Q01.png) .
.
View Solution
