A solid sphere of mass 0.50 kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
The correct Answer is:C
To solve the problem of determining the maximum force that can be applied at the highest point of a solid sphere without causing it to slip, we can follow these steps:
Step 1: Identify the parameters
- Mass of the sphere (m) = 0.50 kg
- Coefficient of static friction (μ) = 2/7
- Gravitational acceleration (g) = 9.81 m/s² (for calculations, we can use g ≈ 10 m/s² for simplicity)
Step 2: Calculate the normal force (N)
The normal force acting on the sphere is equal to its weight:
N=mg=0.50kg×10m/s2=5N
Step 3: Calculate the maximum static friction force (f_max)
The maximum static friction force can be calculated using the formula:
fmax=μN
Substituting the values:
fmax=27×5N=107N≈1.43N
Step 4: Set up the equations of motion
When a force F is applied at the highest point of the sphere, it will cause both translational and rotational motion. The translational acceleration a of the center of mass and the angular acceleration α are related through the radius r of the sphere:
a=αr
Step 5: Apply Newton's second law for translation
The net force acting on the sphere in the horizontal direction is:
F−f=ma
Where f is the friction force opposing the motion.
Step 6: Apply the torque equation
The torque τ about the center of mass due to the applied force F and the friction force f is:
τ=F⋅r−f⋅r=Iα
For a solid sphere, the moment of inertia I is:
I=25mr2
Thus, we can write:
F⋅r−f⋅r=25mr2⋅ar
This simplifies to:
F−f=25ma
Step 7: Solve the equations
Now we have two equations:
1. F−f=ma (1)
2. F−f=25ma (2)
From (1) and (2), we can equate the right-hand sides:
ma=25ma
This implies:
F−f=25ma
Step 8: Relate the forces
From the static friction condition, we know that:
f≤fmax
Substituting fmax=107N:
F−107=25ma
Step 9: Substitute a
Using a=57F from the earlier equations, we can substitute back:
F−107=25m(57F)
This leads to:
F−107=27F
Step 10: Solve for F
Rearranging gives:
F−27F=107
57F=107
F=2N
Conclusion
The maximum force that can be applied at the highest point in the horizontal direction without causing the sphere to slip is:
Fmax=2N
- Mass of the sphere (m) = 0.50 kg
- Coefficient of static friction (μ) = 2/7
- Gravitational acceleration (g) = 9.81 m/s² (for calculations, we can use g ≈ 10 m/s² for simplicity)
The normal force acting on the sphere is equal to its weight:
N=mg=0.50kg×10m/s2=5N
The maximum static friction force can be calculated using the formula:
fmax=μN
Substituting the values:
fmax=27×5N=107N≈1.43N
When a force F is applied at the highest point of the sphere, it will cause both translational and rotational motion. The translational acceleration a of the center of mass and the angular acceleration α are related through the radius r of the sphere:
a=αr
The net force acting on the sphere in the horizontal direction is:
F−f=ma
Where f is the friction force opposing the motion.
The torque τ about the center of mass due to the applied force F and the friction force f is:
τ=F⋅r−f⋅r=Iα
For a solid sphere, the moment of inertia I is:
I=25mr2
Thus, we can write:
F⋅r−f⋅r=25mr2⋅ar
This simplifies to:
F−f=25ma
Now we have two equations:
1. F−f=ma (1)
2. F−f=25ma (2)
ma=25ma
This implies:
F−f=25ma
From the static friction condition, we know that:
f≤fmax
Substituting fmax=107N:
F−107=25ma
Using a=57F from the earlier equations, we can substitute back:
F−107=25m(57F)
This leads to:
F−107=27F
Rearranging gives:
F−27F=107
57F=107
F=2N
The maximum force that can be applied at the highest point in the horizontal direction without causing the sphere to slip is:
Fmax=2N
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -214videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
A solid sphere of mass 3kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface? (in N)
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 A0.15mgB0.05mgC0.1mgD0.45mg
A0.15mgB0.05mgC0.1mgD0.45mg
A body of mass 5kg is under the action of 50N on the horizontal surface. If coefficient of friction in between the surfaces is one, the distance it travels in 3 s is
View SolutionA body of mass 10kg is under the action of 138N on the horizontal surface. If coefficient of friction in between the surfaces is one, the distance it travels in 10s in metre is
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
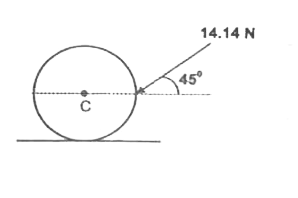
View SolutionA uniform sphere of mass 20kg and radius 10cm is placed on a rough horizontal surface . The coefficient of friction between the sphere and the surface is 0.5.If a force of magnitude 14.14 N is applied on the sphere at an angle of 45∘ with horizontal as shown in the figure, calculate
(a) frictional force
(b) acceleration of the sphere
(c ) angular acceleration of the sphere
 View Solution
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 View Solution
View SolutionA block of mass 70 kg is kept on a rough horizontal surface and coefficient of static friction between block and surface is 0.4 . A man is trying to pull the block by applying a horizontal force .The net contact force exerted by the surface on the block is F , then:
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View Solution

