A solid spherical ball of radius 30 cm and mass M is connected to a point A on wall with a thread and freely rotate about its central axis with angular velocity 60 rad/sec. If the ball is resting onthe vertical face of a wall, what time will elapse before it comes to rest ? The coefficient of friction between wall and ball is 0.25 and inclination of thread to vertical is 15∘.
The correct Answer is:[10.96 sec]
Step by step video, text & image solution for A solid spherical ball of radius 30 cm and mass M is connected to a point A on wall with a thread and freely rotate about its central axis with angular velocity 60 rad//sec. If the ball is resting onthe vertical face of a wall, what time will elapse before it comes to rest ? The coefficient of friction between wall and ball is 0.25 and inclination of thread to vertical is 15^(@). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - MCQ16videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem81videos
NEWTONS LAWS OF MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved1videos
WORK, ENERGY AND POWER
Similar Questions
A solid spherical ball of radius 59m is connected to a point A on the wall with the help of a string which makes an angle θ=45∘ with the vertical. The sphere can rotate freely about its central axis and it is set into rotational motion against the vertical face of the wall with an angular velocity face of the wall with an angular velocity 100 rad s−1. In how much time (in s) will it come to rest ? [μ=0.1]
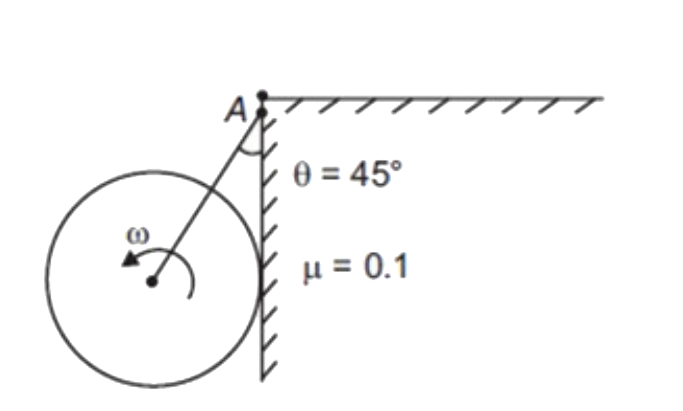 View Solution
View SolutionFrom a point on a smooth floor of a room a ball is shot to hit a wall. The ball then returns back to the point of projection. If the time taken by the ball in returining is twice the time taken to reach the wall, find twice the time taken to reach the wall, find the coefficient of restitution between was and ball.
View Solution
Knowledge Check
- Question 1 - Select One
A spherical solid ball of 5 kg mass and radius 5 cm is rotating about an axis passing through its centre with an angular velocity of 50 rad/sec. The kinetic energy of rotation is
A12 JB10 JC7 JD6.25 J - Question 2 - Select One
A spherical solid ball of 1 kg mass and radius 3 cm is rotating about an axis passing through its centre with an angular velocity of 50 rad s−1. The kinetic energy of rotation is
A4500 JB90 JC910 JD9/20 J - Question 3 - Select One
A girl throws a ball with an initial velocity v at an angle 45∘. The ball strikes a smooth vertical wall at a horizontal distance d from the girl and after rebound returns to her hands. What is the coefficient of restitution between wall and ball ? (v2>dg)
Av2−gdgdBgdv2−gdCgdv2Dv2gd
A small ball of mass m=1 g is placed at the bottom of a watch glass of radius R=1 m. It is displaced by h=1 cm along the glass surface and released. Calculate the total distance deseribed by it before it comes to rest at the bottom, if μ=0.1 is the coefficient of friction between the ball and the watch glass.
View SolutionA ball of radius R=20cm has mass m=0.75kg and moment of inertia (about its diameter ) I=0.0125kgm2. The ball rolls without sliding over a rough horizontal floor with velocity v0=10ms−1 towards a smooth vertical wall if coefficient of restitution between the wall and the ball is e=0.7, calculate velocity v of the ball long after the collision. (g=10ms−2)
View SolutionA ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball long after the collision.
View SolutionA ball is dropped from a height of 3m. If coefficient of restitution between the surface and ball is 0.5, then the total distance covered by the before it comes to rest is
View SolutionA ball of mass m and radius r rolls inside a fixed hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .View Solution
.View Solution

