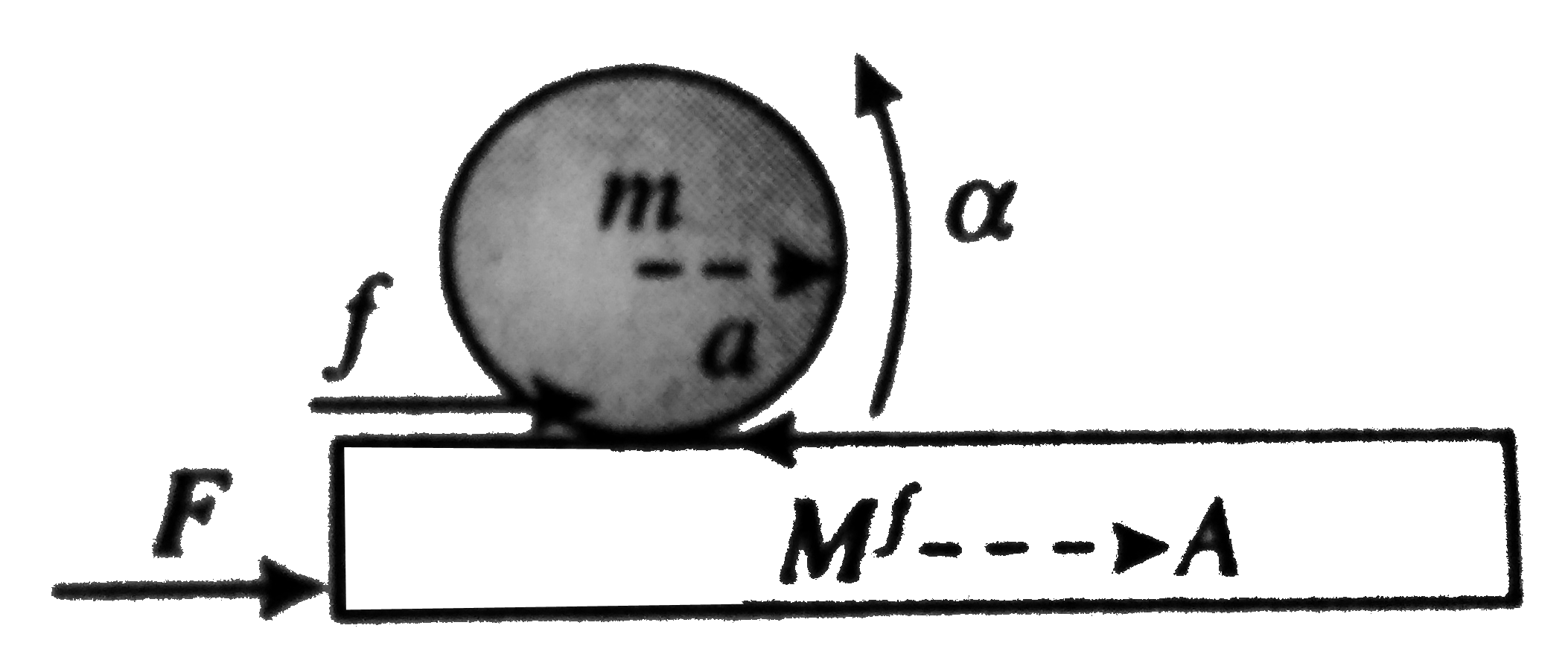
A sphere of mass $m$ and radius $r$ is placed on a rough plank of mass $M$ . The system is placed on a smooth horizontal surface. A constant force $F$ is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{2 F}{7 M + 2 m}$

For $M : F - f = M A$
Form, $f = m a$
$= \frac{2}{5} (m r^{2} . a)$
For pure rolling
$a + α . r = A$
From these quations we have $a = \frac{2 F}{7 M + 2 m}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Acceleration of the plank is
A $\frac{3 F}{16 m}$
B $\frac{11 F}{8 m}$
C $\frac{9 F}{4 m}$
DZero
Question 2 - Select One
Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Friction force acting between the sphere and the plank is
A $\frac{F}{8}$
B $\frac{3 F}{8}$
C $\frac{5 F}{8}$
D $\frac{7 F}{8}$
Question 3 - Select One

A uniform solid cylinder of mass $m$ and radius $R$ is placed on a rough horizontal surface. A horizontal constant force $F$ is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
A $F / 3 m$
B $2 F / 3 m$
C $4 F / 3 m$
D $5 F / 3 m$

CENGAGE PHYSICS-RIGID BODY DYNAMICS 2-Subjective

Home
Ask Doubt
Profile