A sphere S1 of radius r1 encloses a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additional charges between S1andS2 find the ration of electric flux through S1andS2,
To solve the problem, we need to find the ratio of electric flux through two concentric spheres S1 and S2, where S1 encloses a charge Q and S2 is larger than S1 with no additional charges in between.
1. Understanding Electric Flux:
The electric flux Φ through a closed surface is given by Gauss's law, which states:
Φ=Qencϵ0
where Qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
2. Calculate Electric Flux through Sphere S1:
- Sphere S1 encloses the charge Q.
- Therefore, the electric flux through S1 is:
Φ1=Qϵ0
3. Calculate Electric Flux through Sphere S2:
- Sphere S2 is concentric with S1 and also encloses the same charge Q since there are no additional charges between S1 and S2.
- Thus, the electric flux through S2 is also:
Φ2=Qϵ0
4. Finding the Ratio of Electric Flux:
- Now, we need to find the ratio of the electric flux through S1 to the electric flux through S2:
Ratio=Φ1Φ2=Qϵ0Qϵ0=1
Final Answer:
The ratio of electric flux through S1 and S2 is:
Ratio=1
The electric flux Φ through a closed surface is given by Gauss's law, which states:
Φ=Qencϵ0
where Qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
- Sphere S1 encloses the charge Q.
- Therefore, the electric flux through S1 is:
Φ1=Qϵ0
- Sphere S2 is concentric with S1 and also encloses the same charge Q since there are no additional charges between S1 and S2.
- Thus, the electric flux through S2 is also:
Φ2=Qϵ0
- Now, we need to find the ratio of the electric flux through S1 to the electric flux through S2:
Ratio=Φ1Φ2=Qϵ0Qϵ0=1
The ratio of electric flux through S1 and S2 is:
Ratio=1
Similar Questions
A sphere S1 of radius r enclose a total charge Q. If there is another concentric sphere S2 of radius r2(>r1) and there be no additioanl charges between S1andS2 find the ratio of electric flux through S1andS2
View SolutionS1andS2 are two concentric sphere enclosing charges 2Q and 3Q respectively as shown in the figure. What is the ratio of the electric flux through S1andS2?
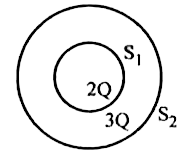
View Solution
Knowledge Check
Conducting sphere of radius R1 is covered by concentric sphere of radius R2. Capacity of this combination is proportional to
AR2−R1R1R2BR2+R1R1R2CR1R2R1+R2DR1R2R2−R1S1andS2 are two hollow concentric spheres enclosing charge Q and 2Q, respectively, as shown in figure. What is the ratio of the electric flux leaving through the surface of S1andS2?
 A14B12C13D23
A14B12C13D23Two metallic s pheres of radii R1 and R2 are connected b y a thin wire. If +q1~and+q_(2) are the charges on the two s pheres then
Aq1/q2 = R1^2/ R2^2Bq1/q2 = R1/ R2Cq1/q2 = R1^3/ R2^3Dq1/q2 =( R1^2 -R2^2/ R1^2+ R2^2)
A thin spherical conducting shell of radius r1 carries a charge Q. Concentric with it is another thin metallic spherical shell of radius r2(r2>r1). Calculate electric field at distance r when (i) r<r1 ,(ii) r1<r<r2 and (iii) r>r2.
What will be the field in above cases if outer shell (a) is given charge q and (b) is earthed ?
View SolutionS1 and S2 are two parallel concentric spheres enclosing charges Q and 2Q respectively as shown in the figure below. What is the ratio of electric flux through S1 and S2 ?

View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.

View SolutionA conducting sphere S1 intersects a closed surface S2 as shown in the figure.A positive charge q is placed at a point P .What is the value of electric flux through the surface S2 ? q P
View SolutionTwo concentric, thin metallic spheres of radii R1 and R2 (R1>R2) bear charges Q1 and Q2 respectively. Then the potential at distance r between R1 and R_(2) will be
View Solution
