A spring of force constant 800N/m has an extension of 5cm. The work done in extending it from 5cm to 15cm is
A
16 J
B
8 J
C
32 J
D
24 J
Video Solution
Text Solution
The correct Answer is:B
(b) W1=12k(5)2×10−4⇒W2=12k(15)2×10−4
where W1 and W2 are the done in extending spring to 5 cm and 15 cm respectively.
W1→2=W2−W1
=12k[(15)2−(5)2]×10−4=12×800(200)×10−4=8J
|
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.2
20 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
Knowledge Check
A spring of force constant 800N/m has an extension of 5cm. The work done in extending it from 5cm to 15cm is
A16 JB8 JC32 JD24 JA spring of force constant 800 N/m has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is:
A16 JB8 JC32 JD24 JA spring of force constant 800Nm−1has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is
A16JB8JC32JD24 J
A spring of force constant 800N/m has an extension of 5cm. The work done in extending it from 5cm to 15cm is
View SolutionA spring of force constant 800Nm−1 is stretched initially by 5cm. The work done in stretching from 5cm to 15cm is
View SolutionA spring with spring constant k is extended from x=0 to x=x1. The work done will be
View SolutionK is the force constant of a spring. The work done in increasing its extension from l1 to l2 will be
View SolutionTwo springs of force constant 100N/m and 150N/m are in series as shown the block is pulled by a distance of 2.5 cm to the right from equilibrium position what is the ratio of work done by the spring at left to the work done by the spring at right:
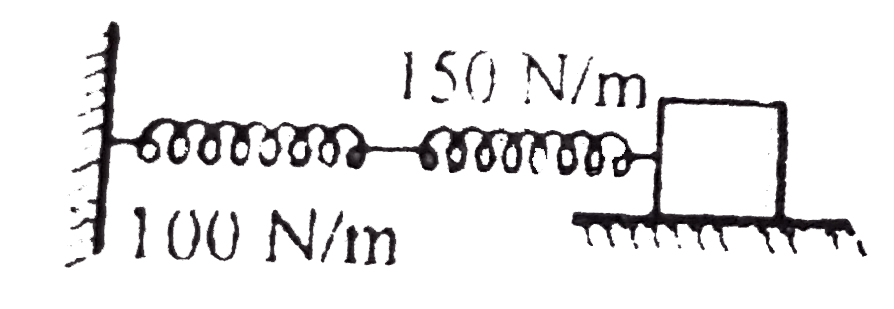
View Solution
