A stone is thrown from a cliff 4.2 m high . At what angle he must incline his rifle in order to cover a maximum range of firing on the ground below . Taken muzzle velocity of bullet =20m/s and g=10ms−2.
To solve the problem of finding the angle at which a stone must be thrown from a cliff to achieve maximum range, we can follow these steps:
Step 1: Understand the problem
We have a stone thrown from a height of 4.2 m with an initial velocity of 20 m/s. We need to find the angle of projection (θ) that maximizes the horizontal range (R) on the ground below.
Step 2: Break down the motion
The motion can be analyzed in two components: horizontal and vertical. The horizontal component of the velocity is given by:
Vx=Vcos(θ)
The vertical component of the velocity is given by:
Vy=Vsin(θ)
Step 3: Calculate the time of flight (t)
The stone will fall a vertical distance of 4.2 m. The equation of motion for vertical displacement is:
h=Vyt−12gt2
Substituting h=4.2 m, Vy=20sin(θ), and g=10m/s2:
4.2=(20sin(θ))t−12(10)t2
This can be rearranged to:
5t2−20sin(θ)t+4.2=0
Step 4: Solve for time of flight (t)
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=5, b=−20sin(θ), and c=4.2:
t=20sin(θ)±√(20sin(θ))2−4⋅5⋅4.22⋅5
t=20sin(θ)±√400sin2(θ)−8410
Step 5: Calculate horizontal range (R)
The horizontal range is given by:
R=Vx⋅t=(20cos(θ))t
Substituting the expression for t:
R=20cos(θ)⋅20sin(θ)+√400sin2(θ)−8410
Step 6: Maximize the range R
To find the angle that maximizes R, we can differentiate R with respect to θ and set the derivative to zero. However, a simpler approach is to use the fact that the angle for maximum range on level ground is 45 degrees. Since the stone is thrown from a height, we need to adjust this angle.
Step 7: Use the discriminant condition
For the quadratic equation in time to have real solutions, the discriminant must be non-negative:
(20sin(θ))2−4⋅5⋅4.2≥0
This gives us the condition for θ.
Step 8: Solve the discriminant condition
Solving the discriminant:
400sin2(θ)−84≥0
sin2(θ)≥84400
sin2(θ)≥0.21
sin(θ)≥√0.21
Step 9: Calculate the angle θ
Using the inverse sine function:
θ=arcsin(√0.21)
Calculating this gives us the angle at which the stone should be thrown to achieve maximum range.
Final Result
After calculating, we find:
θ≈45∘ (adjusted for height)
We have a stone thrown from a height of 4.2 m with an initial velocity of 20 m/s. We need to find the angle of projection (θ) that maximizes the horizontal range (R) on the ground below.
The motion can be analyzed in two components: horizontal and vertical. The horizontal component of the velocity is given by:
Vx=Vcos(θ)
The vertical component of the velocity is given by:
Vy=Vsin(θ)
The stone will fall a vertical distance of 4.2 m. The equation of motion for vertical displacement is:
h=Vyt−12gt2
Substituting h=4.2 m, Vy=20sin(θ), and g=10m/s2:
4.2=(20sin(θ))t−12(10)t2
This can be rearranged to:
5t2−20sin(θ)t+4.2=0
Using the quadratic formula t=−b±√b2−4ac2a:
Here, a=5, b=−20sin(θ), and c=4.2:
t=20sin(θ)±√(20sin(θ))2−4⋅5⋅4.22⋅5
t=20sin(θ)±√400sin2(θ)−8410
The horizontal range is given by:
R=Vx⋅t=(20cos(θ))t
Substituting the expression for t:
R=20cos(θ)⋅20sin(θ)+√400sin2(θ)−8410
To find the angle that maximizes R, we can differentiate R with respect to θ and set the derivative to zero. However, a simpler approach is to use the fact that the angle for maximum range on level ground is 45 degrees. Since the stone is thrown from a height, we need to adjust this angle.
For the quadratic equation in time to have real solutions, the discriminant must be non-negative:
(20sin(θ))2−4⋅5⋅4.2≥0
This gives us the condition for θ.
Solving the discriminant:
400sin2(θ)−84≥0
sin2(θ)≥84400
sin2(θ)≥0.21
sin(θ)≥√0.21
Using the inverse sine function:
θ=arcsin(√0.21)
Calculating this gives us the angle at which the stone should be thrown to achieve maximum range.
After calculating, we find:
θ≈45∘ (adjusted for height)
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (1)
8 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS (2)
9 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
A machine gun is mounted on the top of a tower of height h=100 m. At what angle should the gun be inclined to cover a maximum range of firing on the ground below ?The muzzle speed of the bullet is u=150ms−1 and g=10ms−2 .
View SolutionA machine gun is mounted on the top of a tower of height h. At what angle should the gun be inclined to cover a maximum range of firing on the ground below ? The muzzle speed of bullet is 150ms−1. Take g=10ms−2.
View Solution
Knowledge Check
The maximum range of a gun on horizontal terrain is 25 km. If g= 10 ms−2, the muzzle velocity of the shell
A250ms−1B2500ms−1C25ms−1D500ms−1A missile is fired for maximum range with an initial velocity of 20m/s. If g=10m/s2, the range of the missile is
A50mB60mC20mD40mA ball is thrown from the ground with a velocity of 20√3 m/s making an angle of 60∘ with the horizontal. The ball will be at a height of 40 m from the ground after a time t equal to (g=10ms−2)
A√2 secB√3 secC2 secD3 sec
A machine gun is mounted on the top of a tower 60m At what angle showld the gun be inclined to cver a vaximu range of firing on the groun below? The muzzle speed of the bullet is 90ms−1 take g=10ms1.
View SolutionThe maximum range of a bullet fired from a toy pistol mounted on a car at rest is R0=40m. What will be the acute angle of inclination of the pistol for maximum range when the car is moving in the direction of firing with uniform velocity V=20m/s, on a horizontal surface? (g=10m/s2)
View SolutionThe range of a rifle bullet on level ground is 60 m. The range (in m) upon incline of 30∘ is . (Take g=10m/s2)
View SolutionA bullet of mass 10 g is fired from a gun of mass 1 kg with recoil velocity of gun 5 m/s. The muzzle velocity will be
View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
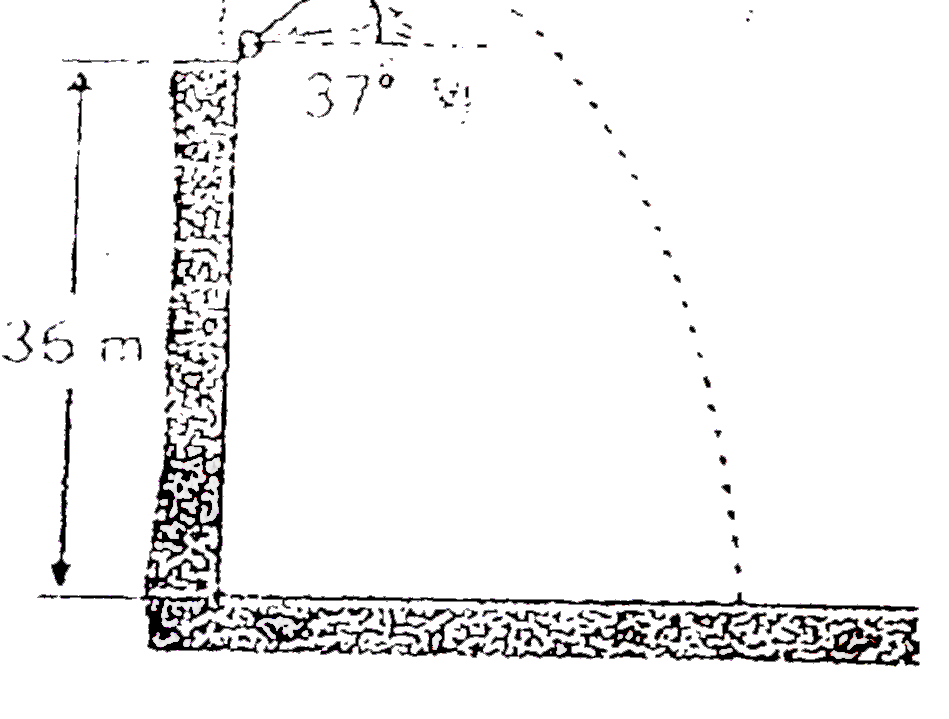 :
:
View Solution
