A string is fixed at both end transverse oscillations with amplitude are excited. Which of the following statements are correct ?
(a) Energy of oscillations in the string is directly proportional to tension in the string
(b) Energy of oscillations in nth overtone will be equal to times of that in first overtone
(c) Average kinetic energy of string (over an oscillation period) is half of the oscillation energy
(d) None of the above
The correct Answer is:A, C
To solve the problem regarding the transverse oscillations of a string fixed at both ends, we will analyze each statement provided in the question step by step.
Step 1: Analyze the Energy of Oscillation in the String
The energy of oscillation in a string can be expressed in terms of its amplitude, tension, and mass per unit length. The formula for the energy (E) in a vibrating string is given by:
E=12TA2
where:
- T is the tension in the string,
- A is the amplitude of oscillation.
From this equation, we can see that the energy of oscillation is directly proportional to the tension in the string. Therefore, the first statement is correct.
Step 2: Analyze the Energy in Terms of Overtone
The fundamental frequency (first harmonic) of a string fixed at both ends is given by:
f0=12L√Tμ
where:
- L is the length of the string,
- μ is the mass per unit length of the string.
The frequency of the nth overtone (which is the (n+1)th harmonic) can be expressed as:
fn=(n+1)f0
The energy associated with the nth overtone can be expressed as:
En∝f2n
This leads us to:
En∝(n+1)2
This means that the energy of the nth overtone is proportional to (n+1)2, not n2. Therefore, the second statement is incorrect.
Step 3: Analyze the Average Kinetic Energy
The average kinetic energy of the oscillating string can be derived from the total energy of oscillation. The average kinetic energy (K.E.) in a simple harmonic motion is given by:
K.E.=12E
This implies that the average kinetic energy over one oscillation period is half of the total oscillation energy. Therefore, the third statement is correct.
Conclusion
Based on the analysis:
- The first statement is correct: The energy of oscillation in the string is directly proportional to the tension in the string.
- The second statement is incorrect: The energy in the nth overtone is proportional to (n+1)2, not n2.
- The third statement is correct: The average kinetic energy is half of the total oscillation energy.
Final Answer
The correct statements are:
- A: Correct
- B: Incorrect
- C: Correct
The energy of oscillation in a string can be expressed in terms of its amplitude, tension, and mass per unit length. The formula for the energy (E) in a vibrating string is given by:
E=12TA2
where:
- T is the tension in the string,
- A is the amplitude of oscillation.
The fundamental frequency (first harmonic) of a string fixed at both ends is given by:
f0=12L√Tμ
where:
- L is the length of the string,
- μ is the mass per unit length of the string.
fn=(n+1)f0
The energy associated with the nth overtone can be expressed as:
En∝f2n
This leads us to:
En∝(n+1)2
This means that the energy of the nth overtone is proportional to (n+1)2, not n2. Therefore, the second statement is incorrect.
The average kinetic energy of the oscillating string can be derived from the total energy of oscillation. The average kinetic energy (K.E.) in a simple harmonic motion is given by:
K.E.=12E
This implies that the average kinetic energy over one oscillation period is half of the total oscillation energy. Therefore, the third statement is correct.
Based on the analysis:
- The first statement is correct: The energy of oscillation in the string is directly proportional to the tension in the string.
- The second statement is incorrect: The energy in the nth overtone is proportional to (n+1)2, not n2.
- The third statement is correct: The average kinetic energy is half of the total oscillation energy.
The correct statements are:
- A: Correct
- B: Incorrect
- C: Correct
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Assertion - Reasoning6videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension55videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct144videos
SUPERPOSITION AND STANDING WAVES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 241videos
THERMODYNAMICS
Similar Questions
A metal sphere is hung by a string fixed to a wall. The forces acting on the sphere are shown in fig Which of the following statements are correct?
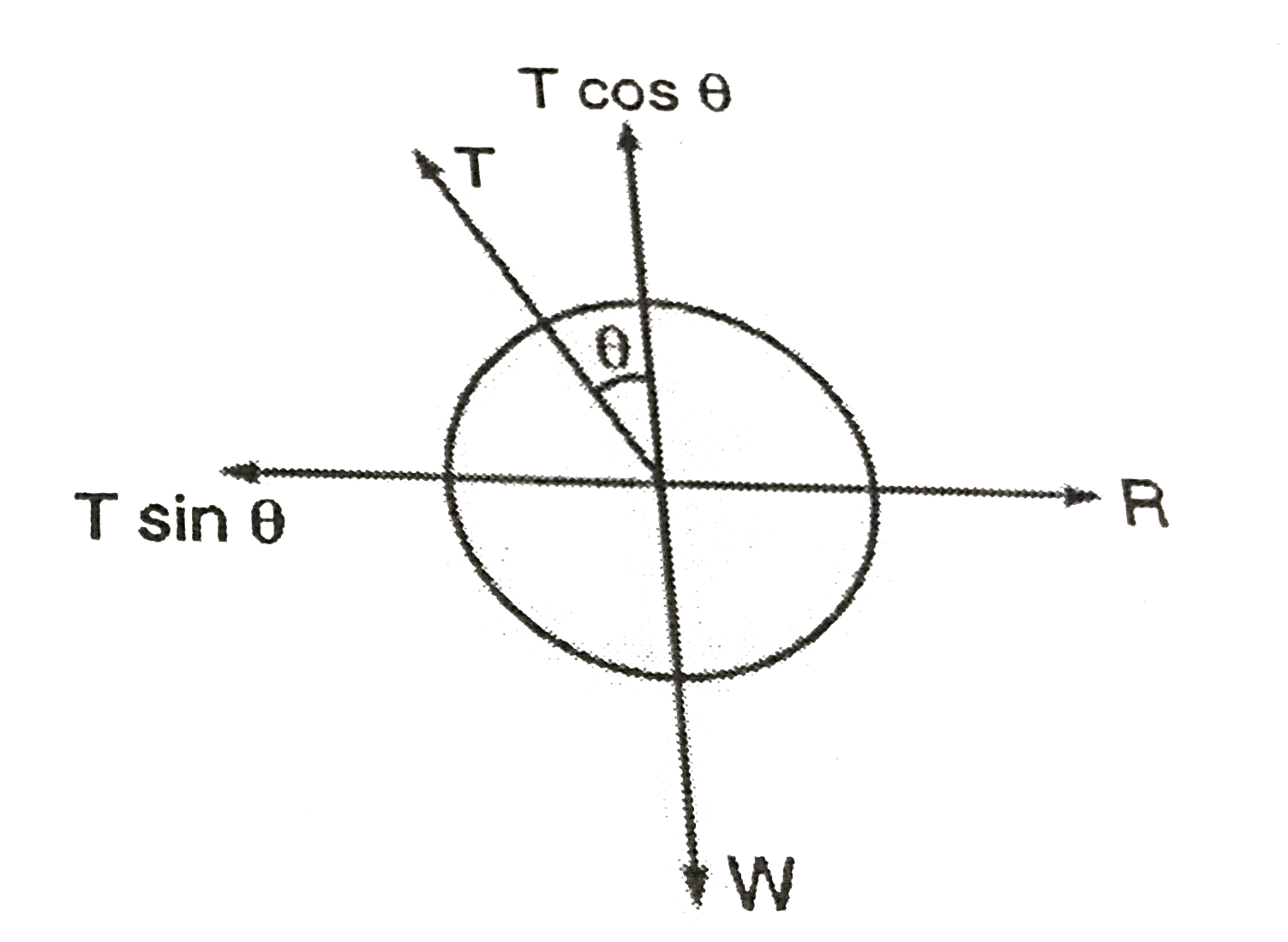 View Solution
View SolutionTwo fixed charges −2Q and +Q are located at points (−3a,0) and (+3a,0) respectively. Then which of the following statement is correct?
View Solution
Knowledge Check
- Question 1 - Select One
The amplitude of em wave in vacuum is doubled with no other changes made to wave. As a result of this doubling of the amplitude, which of the following statement is correct.
AThe speed of wave propagation changes onlyBThe frequency of the wave change onlyCThe wavelength of the wave changes onlyDNone of these
A string fixed at both ends first oscillates in its fundamental mode then in second harmonic mode.Then match the following.
 View Solution
View SolutionA rod is made of uniform material and has non-uniform cross section. It is fixed at both the ends as shown and heated at mid-section. Which of the following are not correct?
 View Solution
View SolutionWhich of the following statement is not correct exciting stage of neuron’?
View SolutionA stretched string of length L , fixed at both ends can sustain stationary waves of wavelength λ Which of the following value of wavelength is not possible ?
View SolutionFigure shown a clamped metal string of length 30cm and linear mass density 0.1kg/m. Which is taut at a tension of 40N. A small rider ( piece of paper ) is placed on string at point P as shown. An external vibrating tuning fork is brought near this string and oscillations of rider are carefully observed.
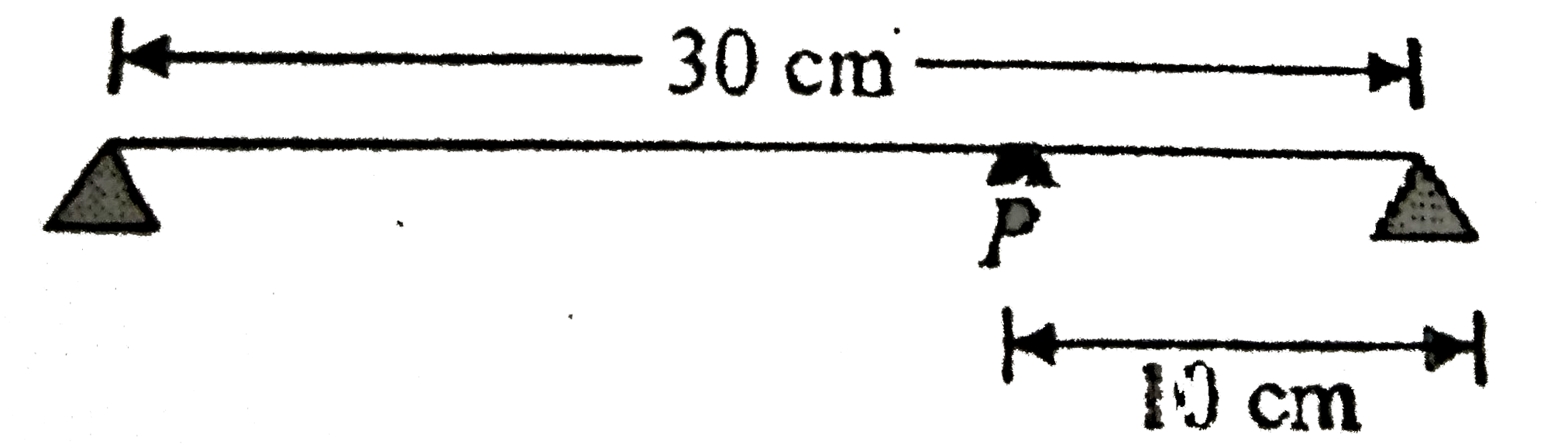
At which of the following frequencies the point P on string will have maximum oscillation amplitude among all points on string :View SolutionA ball of mass m is attached to a string whose other end is fixed. The system is free to rotate in vertical plane. When the ball swings, no work is done on the ball by the tension in the string. Which of the following statement is the correct explanation?
View SolutionA string of length L is stretched along the x-axis and is rigidly clamped at its two ends. It undergoes transverse vibration. If n an integer, which of the following relations may represent the shape of the string at any time :-
View Solution

