A symmetric lamina of mass M consists of a square shape with a semicircular section over each of the edge of the square as in fig. The side of the square is 2a.
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma2. The moment of inertia of the lamina about the tangent AB in the plane of lamina is.
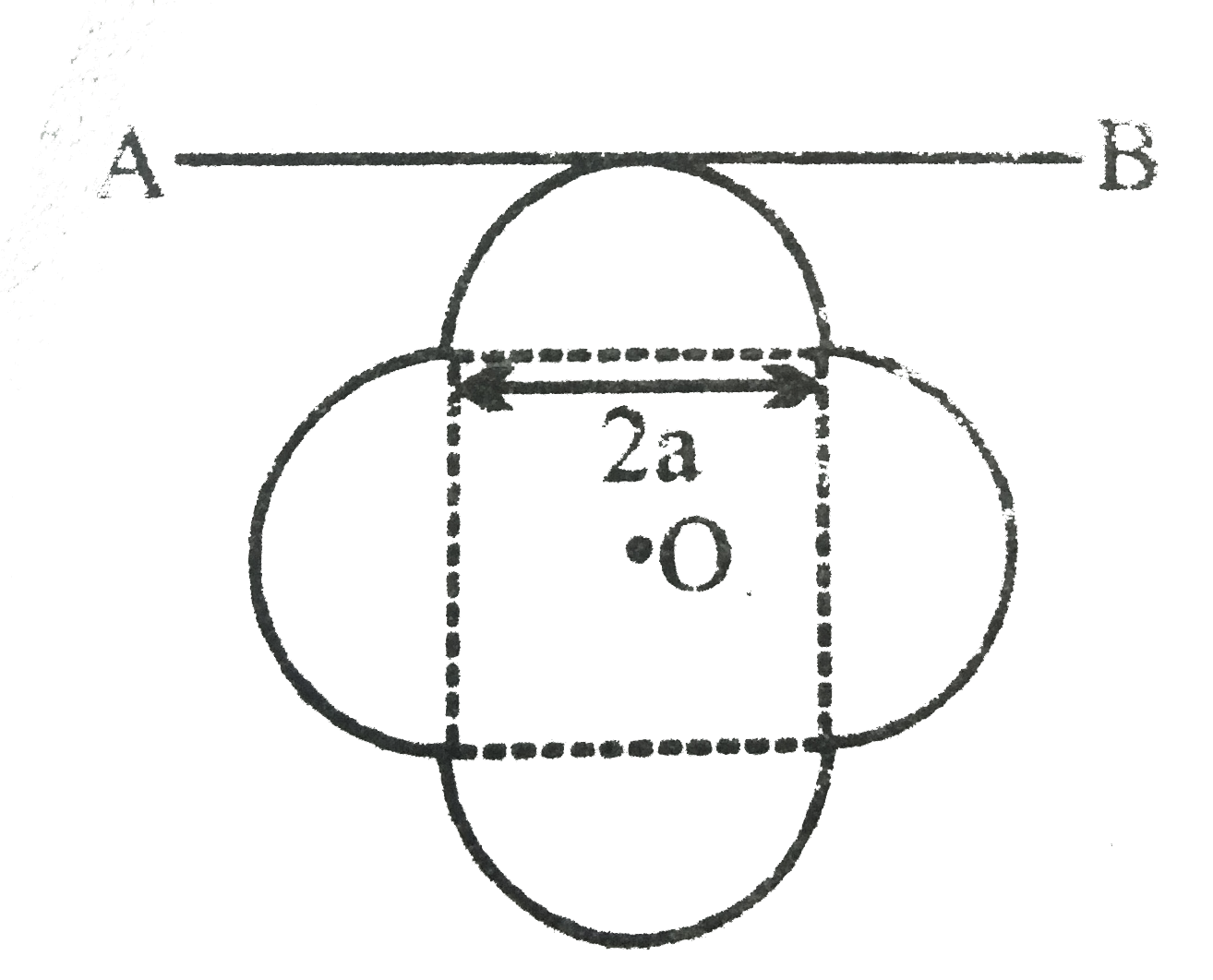 .
.
Assuming symmetric lamina to be in xy plane we will have
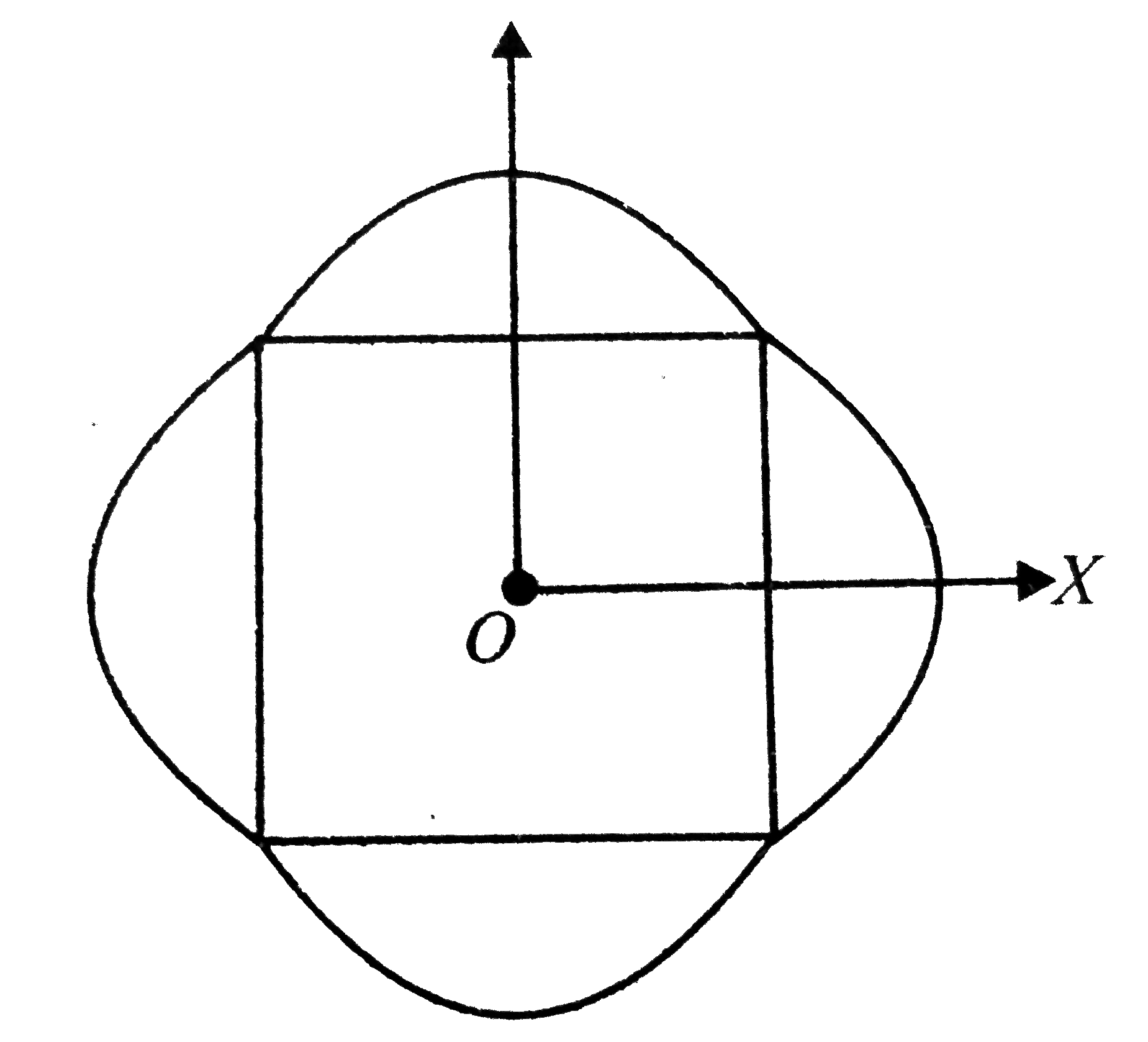
Ix=Iy(since the mass distribution is the mass about the x-axis and y-axis)
Ix=Iy=Iz (perpendiclar axis theorem)
it is given that
Iz=1.6Ma2
Hence Ix=Iy=Iz2=0.8Ma2
Now according to the paralel axis theorem, we get
IAB=IXTM(2a)2
=0.8Ma2+4Ma2=4.8Ma2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - True/False4videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - SCQ_TYPE29videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Integer7videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A symmetric lamina of mass M consists of a square shape with a semicircular section over of the edge of the square as shown in fig. p-10. The side of the square is 2a. The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma2. The moment of inertia of the lamina is ......
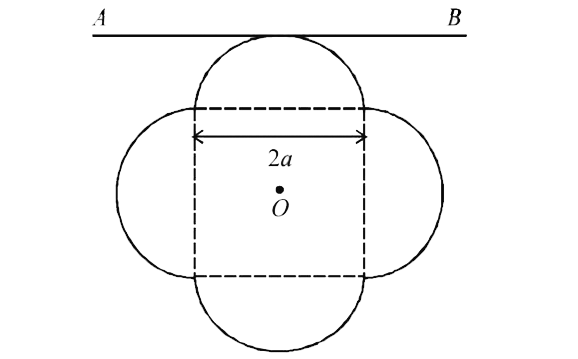 View Solution
View SolutionThe moment of inertia of a disc about an axis through its centre and perpendicular to its plane is 12MR2 . Its moment of inertia about any diameter will be __________
View Solution
Knowledge Check
- Question 1 - Select One
The moment of inertia of a circular disc about an axis passing through its centre and perpendicular to the plane is 4kgm2 . Its moment of inertia about the diameter is
A2kgm2B6kgm2C4kgm2D8kgm2 - Question 2 - Select One
The moment of inertia of a disc an axis passing through its centre and perpendicular to its plane is I kg m2 . Its moment of inertia about an axis coincident with the tangent to it is
AIB54IC52ID3I - Question 3 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is I. What is the moment of inertia about its diameter ?
View SolutionThe moment of inertia of a square plate of mass 4kg and side 1m about an axis passing through its centre and perpendicular to its plane is
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is I. What is the moment of inertia about its diameter?
View Solution

