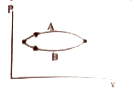
A system goes from state A to B via two processes I and II, as shown in Fig. 12.25, How are δμ1 and δμ2 (the changes in internal energies in the processes I and II) related to each other ?
To solve the problem of how the changes in internal energies (ΔU1 and ΔU2) during two different processes (I and II) from state A to state B are related, we can follow these steps:
1. Understand the Concept of Internal Energy:
- Internal energy (U) is a property of a system that depends only on its state, not on how it reached that state. This means that internal energy is a state function.
2. Identify the States:
- We have two states: A (initial state) and B (final state). Both processes I and II start at state A and end at state B.
3. Define the Changes in Internal Energy:
- For process I, the change in internal energy is denoted as ΔU1 = U_B - U_A.
- For process II, the change in internal energy is denoted as ΔU2 = U_B - U_A.
4. Apply the State Function Property:
- Since internal energy is a state function, the change in internal energy only depends on the initial and final states, not on the path taken.
- Therefore, regardless of whether the system goes from A to B via process I or process II, the change in internal energy will be the same.
5. Conclude the Relationship:
- Since both processes have the same initial and final states, we can conclude that:
ΔU1=ΔU2
Final Answer
Thus, the relationship between the changes in internal energies during the two processes is:
ΔU1=ΔU2
- Internal energy (U) is a property of a system that depends only on its state, not on how it reached that state. This means that internal energy is a state function.
- We have two states: A (initial state) and B (final state). Both processes I and II start at state A and end at state B.
- For process I, the change in internal energy is denoted as ΔU1 = U_B - U_A.
- For process II, the change in internal energy is denoted as ΔU2 = U_B - U_A.
- Since internal energy is a state function, the change in internal energy only depends on the initial and final states, not on the path taken.
- Therefore, regardless of whether the system goes from A to B via process I or process II, the change in internal energy will be the same.
- Since both processes have the same initial and final states, we can conclude that:
ΔU1=ΔU2
Thus, the relationship between the changes in internal energies during the two processes is:
ΔU1=ΔU2
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A system goes from A to B via two processes I and II as shown in the figure. If ΔU1 and ΔU2 are the changes in the internal energies in the processes I and II respectively, then -
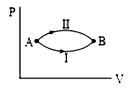 AΔU1=ΔU2Brelation between ΔU1andΔU2 cannot be determinedCΔU2>ΔU1DΔU2<ΔU1
AΔU1=ΔU2Brelation between ΔU1andΔU2 cannot be determinedCΔU2>ΔU1DΔU2<ΔU1 - Question 2 - Select One
A system goes from A and B via two processes. I and II as shown in figure. If ΔU1andΔU2 are the changes in internal enregies in the processes I and II respectively, then
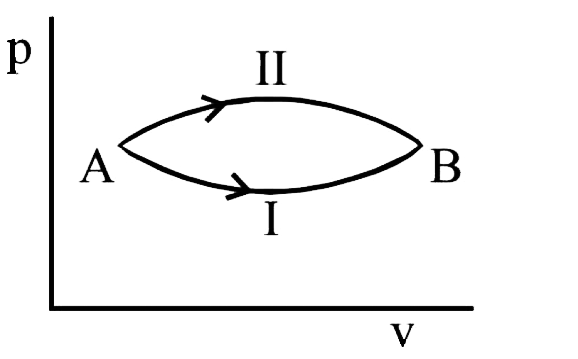 Arelation between ΔU1and Δu2 can not be determinedBΔU1=ΔU2CΔU2<ΔU1DΔU2>ΔU1
Arelation between ΔU1and Δu2 can not be determinedBΔU1=ΔU2CΔU2<ΔU1DΔU2>ΔU1 - Question 3 - Select One
Let ΔU1 and ΔU2 be the changes in internal energy of an ideal gas in the processes A and B then
AΔU1>ΔU2BΔU1=ΔU2CΔU1<ΔU2DΔU1≠ΔU2
A system is changed from state A to state B by one path and from B to A by another path. If ΔE1 and ΔE2 are the corresponding changes in internal energy, then
View SolutionA system is changed from state A to state B by one path and from B to A by another path. If ΔE1 and ΔE2 are the corresponding changes in internal energy, then
View SolutionAn ideal gas undergoes an expansion from a state with temperature T1 and volume V1 through three different polytropic processes A,B and C as shown in the P−V diagram. If |ΔEA|,|ΔEB| and |ΔEC| be the magnitude of changes in internal energy along the three paths respectively, then :
 View Solution
View SolutionRefer to let ΔU1 and ΔU2 be the changes in internal energy in the system in process A+B and ΔW be the net work done by the system in the process A+B,
 View Solution
View Solutionconsider two processes on a system on a system as shown in
the volumes in the initial states are the same in the two processes and the volume in the final states are also the same.Let ΔW1andΔW2 be the work done by the sustem in the processes A and B respectively.
 View Solution
View Solution