A tank of height 33.25 cm is completely filled with liquid . An object is placed at the bottom of tank of the axis of concave mirror as shown in the figure. Image of the object is formed 25 cm below the surface of the liquid. What is the focal length of the mirror? 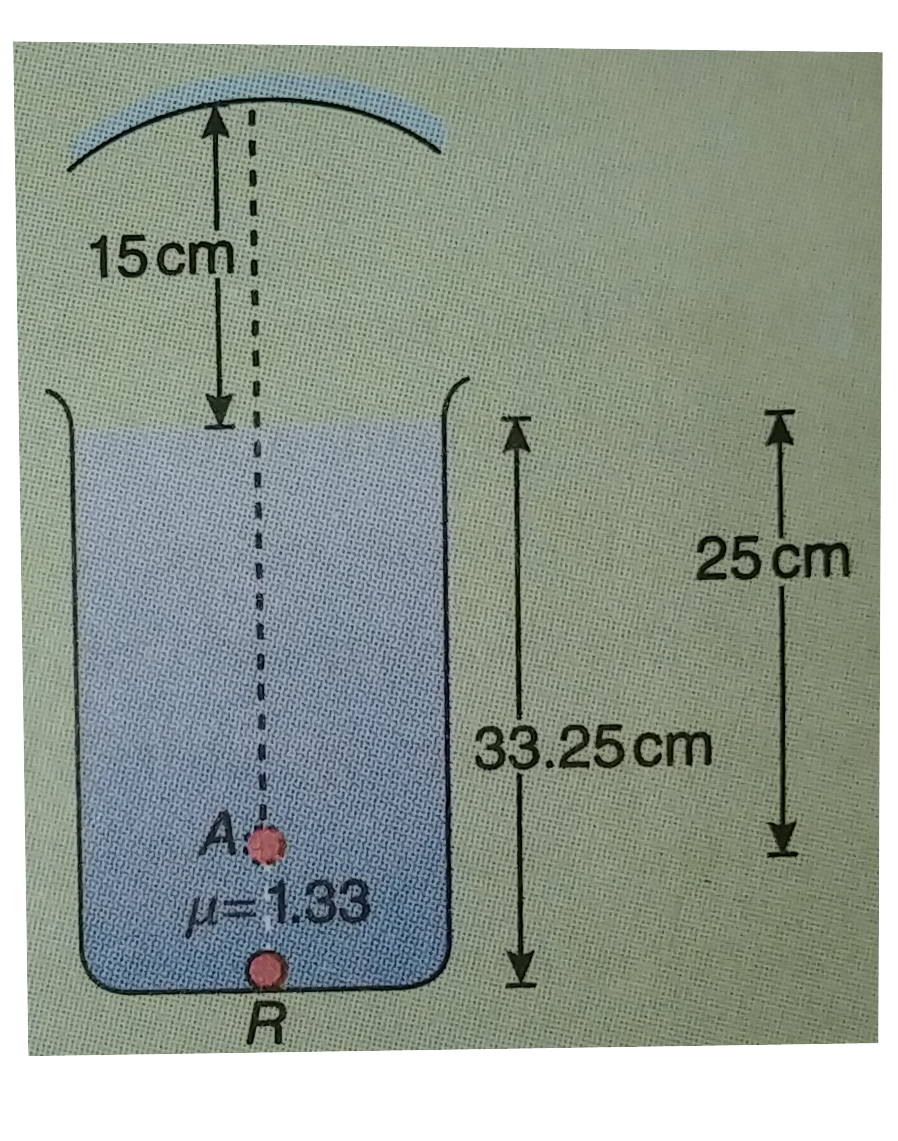
Here , R is the actual position of the object and A is the apparent position of the image.
Therefore, apparent depth of the object =
Here, object distance,
and image distance, v = - (15 + 25)cm = - 40 cm
Applying mirror equation, we get
Therefore, required focal length is 20 cm.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)
25 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
Knowledge Check
A tank of height 33.25 cm is completely filled with liquid (μ = 1.33). An object is placed at the bottom of tank on the axis of concave mirror as shown in the figure. Image of the object is formed 25 cm below the surface of the liquid, then focal length of the mirror is
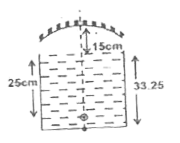 A10 cmB15 cmC20cmD25 cm
A10 cmB15 cmC20cmD25 cmAn object is placed at 15 cm in front of a concave mirror whose focal length is 10 cm. The image formed will be
Amagnified and invertedBmagnified and erectCreduced in size and invertedDreduced in size and erect.An object is placed at a distance of 20 cm from the pole of a concave mirror of focal length 10 cm. The distance of the image formed is
A+20cmB+10CmC−20cmD−10cm
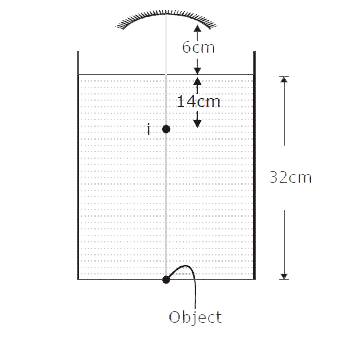
A beaker contains water (μ=4/3) filled to a height of 32 cm. A concave mirror is fixed 6 cm above the surface of water as shown in figure. An object is placed at the bottom of the beaker and its image is formed 14 cm below the surface of water. The focal length of the mirror is
View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionAn object is placed at a distance of 15 cm from a concave mirror and its real image is formed at 30 cm in front of that mirror. The focal length of the mirror is
View SolutionAn object is placed 40 cm from the concave mirror with a focal length of 20 cm . The image formed is :
View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View Solution
