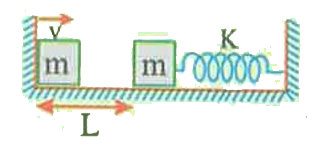
(a) The right block collides with left block and sticks to it. Find amplitude of the resulting SHM.

(b) The block starts from left wall and moves with constant speed v. All collisions are elastic. Find time period of periodic motion.

(a) 
By momentum conservation
2mv=(m+2m)V⇒V=2v3
K.E. of combined block
=12(2m+m)V2=3m2(2v3)2=23mv2
Let A be the amplitude
23mv2=12kA2⇒A=v√4m3k
(b) The block reaches to spring with speed v. The block compresses the spring by distance x such that 12mv2=12kx2. Now block moves toward left, when it leaves contact with spring, its speed is v. The time for which block is in contact with spring t1=T2=π√mk.
Time taken by block to move from left wall to spring and then spring to left wall
t2=Lv+Lv=2Lv
Thus block undergoes periodic motion with time period
t1+t2=π√mk+2Lv.

Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the time period of SHM of the block of mass M
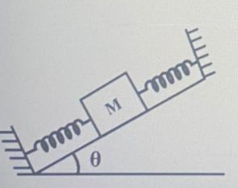 AT=2π√M2KBT=2π√MKCT=2π√2MKDT=2π√M4K
AT=2π√M2KBT=2π√MKCT=2π√2MKDT=2π√M4K - Question 2 - Select One
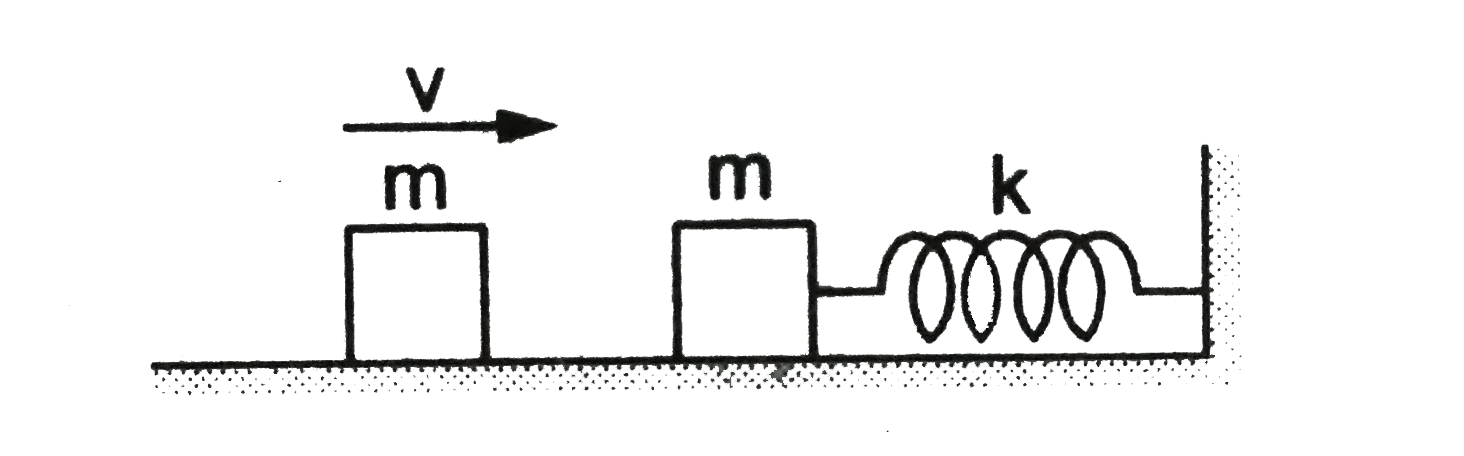
The right block in figure moces at a speed V towards the left block placed in equilibrium. All the surfaces are smooth and all the collisions are elastic. Find the time period motion. Neglect the width of the blocks.
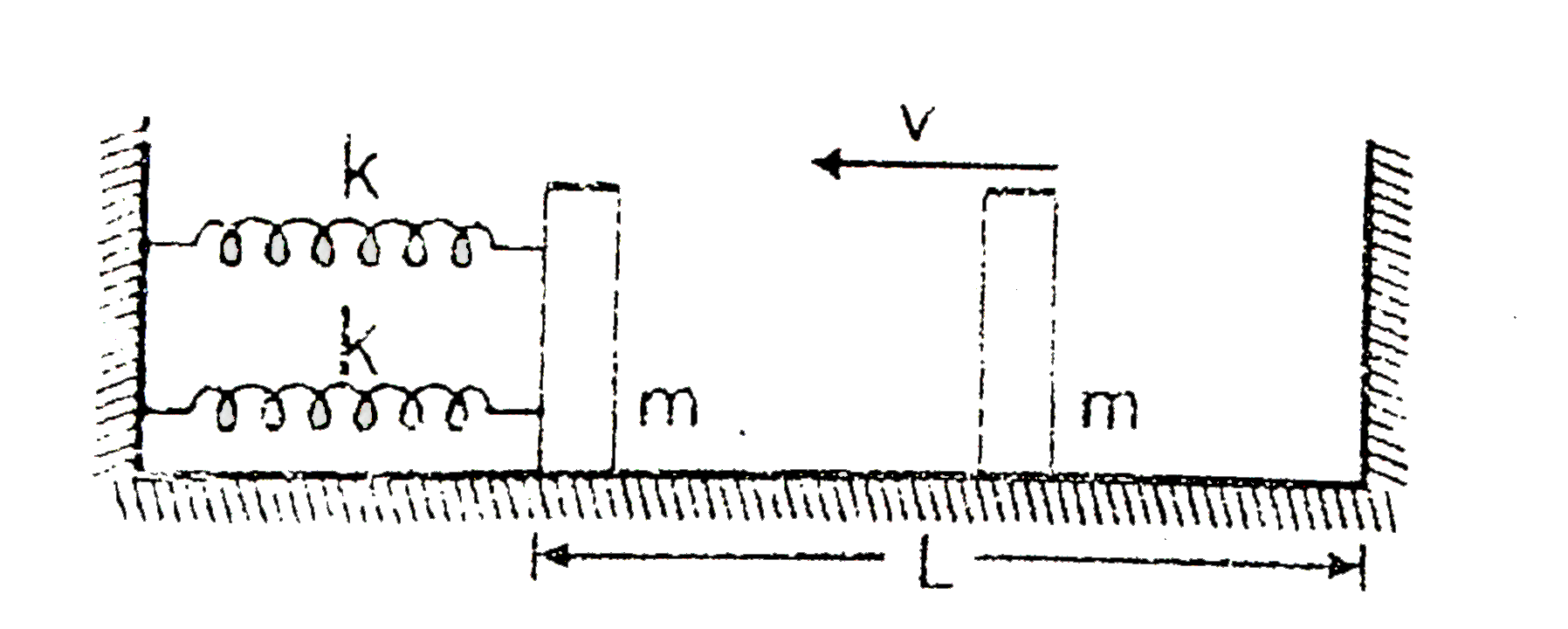 Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv - Question 3 - Select One
The right block in figure moces at a speed V towards the left block placed in equilibrium. All the surfaces are smooth and all the collisions are elastic. Find the time period motion. Neglect the width of the blocks.
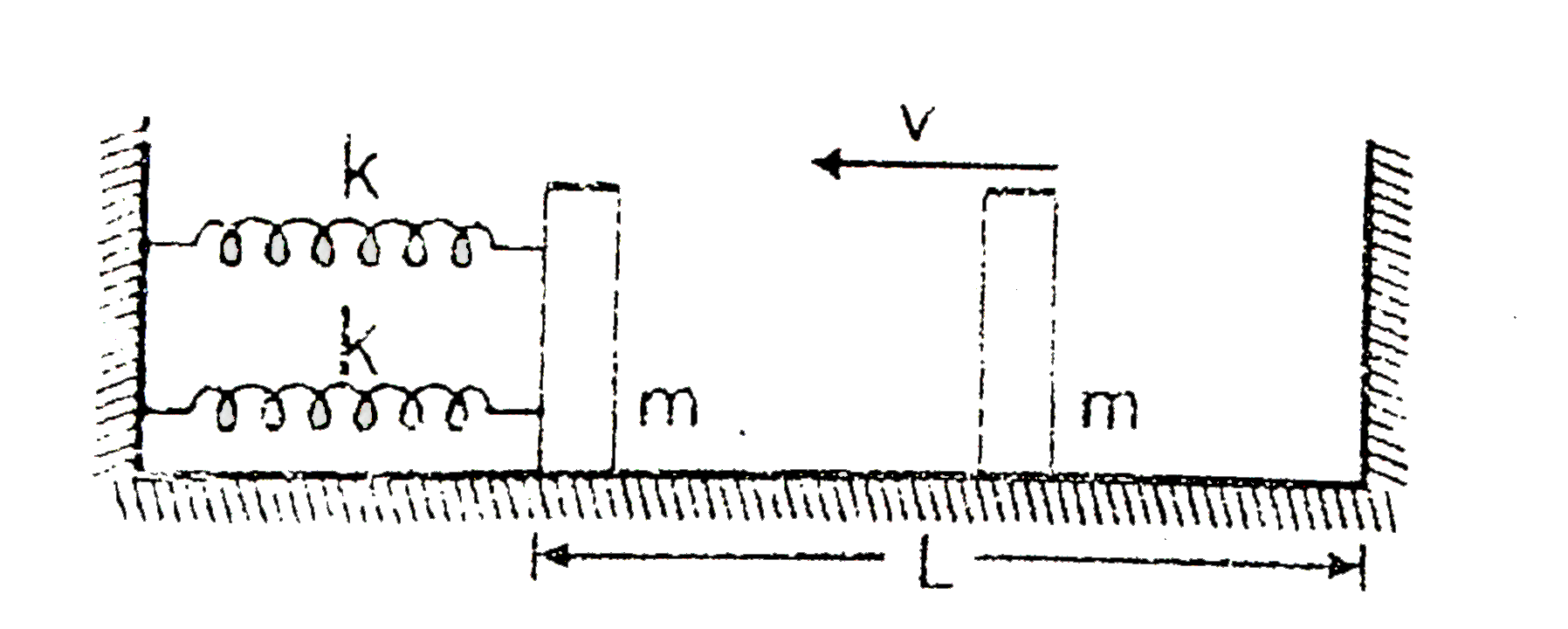 Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
Aπ√m2k+2LvBπ√m2k+LvCπ√m2k−LvDπ√mk+Lv
The left block in figure collides inelastically with the right block and sticks to it. Find the amplitude of the resulting simple harmonic motion.
 View Solution
View SolutionThe left block in figure collides inelastically with the right block and striks to it. Find the amplitude of the resulting simple harmonic motion
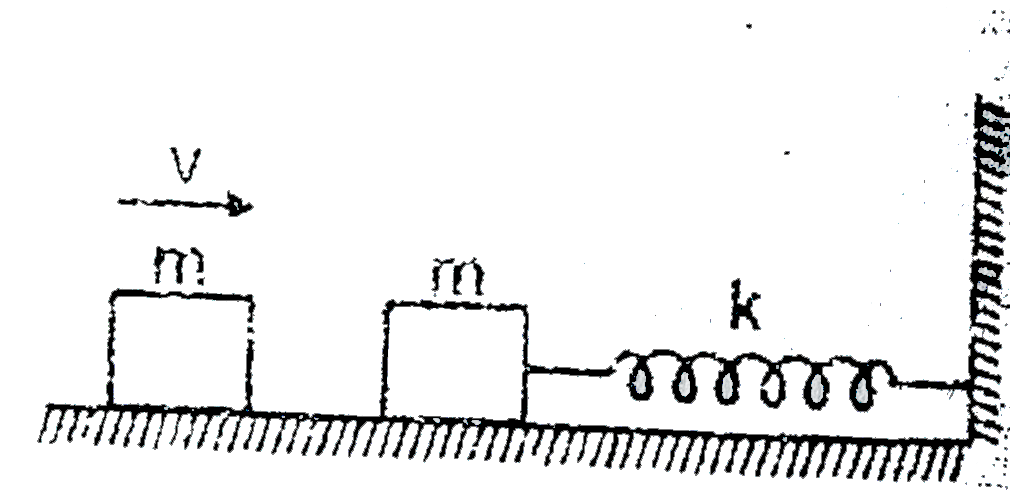 View Solution
View SolutionA block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View SolutionThree blocks of identical masses are placed on a frictionless table as shown . The centre block is at rest , whereas the other two blocks are moving directly towards the stationary block with identical speed v . The centre block is initially closer to the left block than the right one . All collisions are elastic . After long time , which of the following is true .
 View Solution
View SolutionAll the surfaces shown in figure are frictionless. The mass of the car is M, that of the block is mk and the spring has spring constant. Initialy the car and the block are at rest and the spring is stretched through a length x0 when the system is released. a. Find the amplitude of the simple harmonic motion of the blocks and of the car as seen from the road. b. Find the time periods of the two simple harmonic motions.
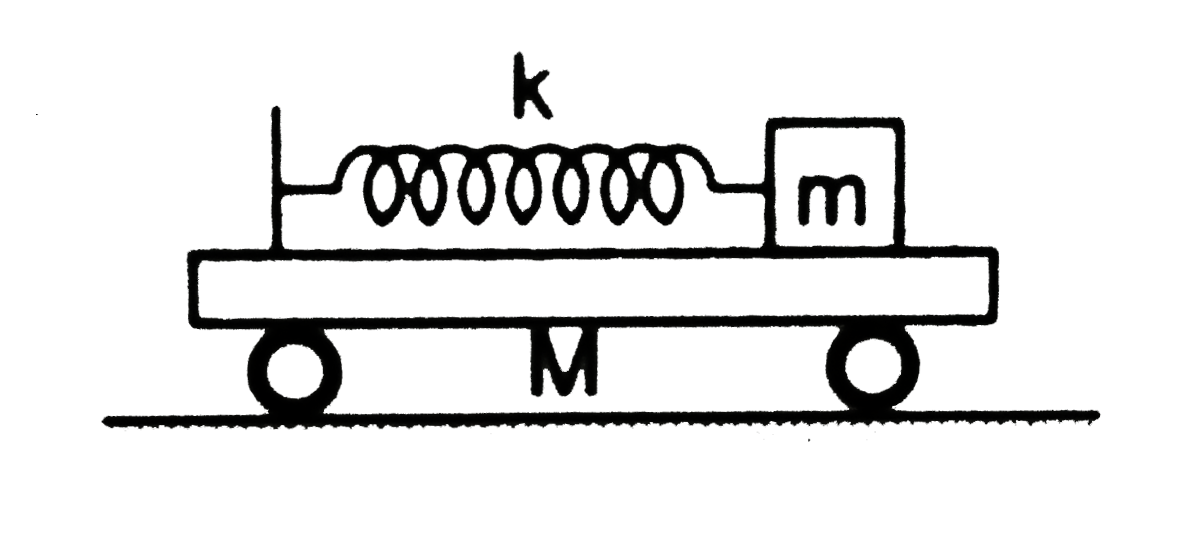 View Solution
View Solution