A thin equi-convex glass lens (refractive index = 1.5) is being placed on the top of a vessel of height h = 20 cm as shown in the figure. A luminous point source is being placed at the bottom of the vessel on the principle axis of the lens. When air is on both sides of the lens, the image of luminous point source is found at a distance 20 cm from the lens outside the vessel. When the air inside the vessel is being replaced by a source is fomed at a distance 30 cm from the lens outside the vessel. The value of μ is

The correct Answer is:1.11
For the first lens,
1v−1u=(μ−1)(1R1−1R2)
120−1−20=(1.5−1)(1R−1−R)⇒R=10cm
For the second case when the vessel is being fillle dwith the liquid then
μairv1−μlu=ug−μlR+μair−μg−R
130−μl−20=1.5−μl10+1−1.5−10
μl20+μl10=320+120−130
3μl20=16
μl=109=1.11
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Single Correct
221 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.7
21 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A thin equiconvex glass lens (μg=1.5) is beign placed on the top of a vessel of height h=20cm as shown figure. A luminous point source is beign placed at the bottom of vessel on the principal axis of the lens. When the air is on both the side of the lens the image of luminous source is formed at a distance of 20cm from the lens out side the vessel. When the air inside the vessel is being replaced by a liquid of refractive index μl the image of the same source is being formed at a distance 30cm from the lens outside the vessel. Find the μl.

View SolutionTwo point objects are placed on principal axis of a thin converging lens. One is 20cm from the lens and other is on the other side of lens at a distance of 40 cm from the lens. The images of both objects coincide. The magnitude of focal length of lens is :-
View SolutionA pin of length 1cm lies along the principle axis of a converging lens, the centre being at a distance of 5,5cm form the lens. The focal length of the lens is 3cm. Find the size of the image.
View SolutionA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionA glass lens of refractive index 1.5 is placed in a trough of liquid. What must be the refractive index of the liquid in order to mark the lens disappear?
View SolutionA pin of length 2.0 cm lies along the principal axis of a converging lens, the centre being at a distance of 11 cm from the lens. The focal length of the lens is 6 cm. Find the size of the image.
View SolutionPlane surface of a thin plano-convex lens is silvered. If a point object is placed on principal axis at a distance 60cm from the lens and fial image is formed at a distance 30cm from the lens on same side. What will be the distance of final imagge from the lens if the plane surface is not silvered.
View SolutionA convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
View SolutionA thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.

Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.
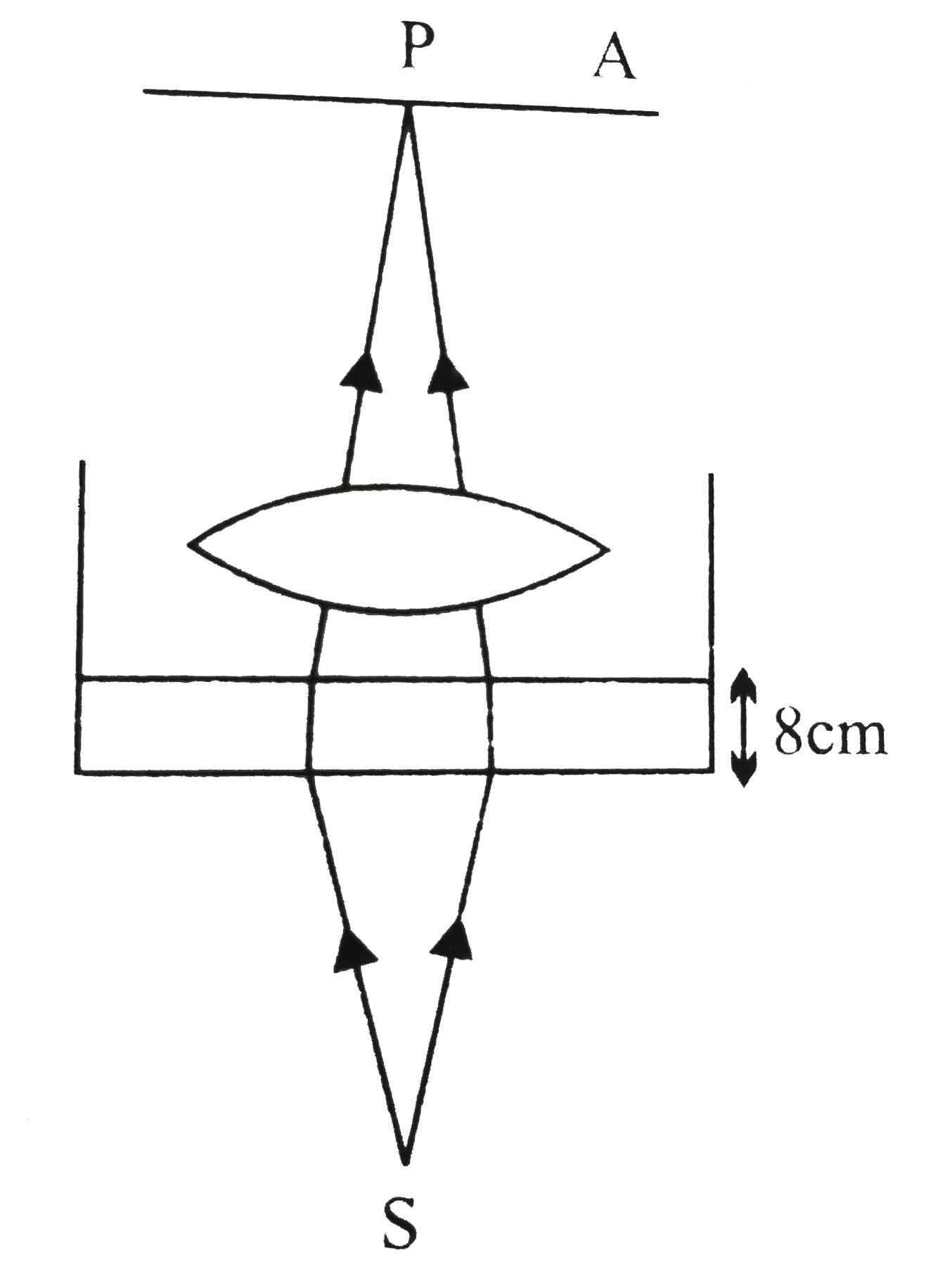
View SolutionA thin convex lens of refractive index μ=1.5 is placed between a point source of Light S and a screen A, shown in figure,. Light rays from the source S are brought to focus on the screen A, forming a point image P. The distance SP is equal to 50cm. Water (μ=4/3) is now poured into a vessel interposed between the object and the lens, and it is observed that when the water level is 8cm the screen has to be moved up by a distance of 6cm in order to get a sharp image. Find the focal length of the lens.
View Solution
