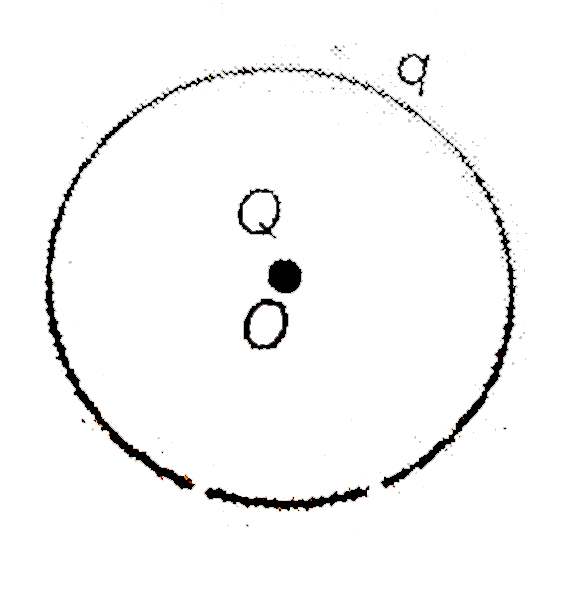
A thin insulating wire is stretched along the diameter of an insulated circular hoop of radius R. A small bead of mass m and charge –q is threaded onto the wire. Two small identical charge +Q are tied to the hoop at points opposite to each other, so that the diameter passing through them is perpendicular to the thread (see figure). The bead is released at a point which is a distance x_0, from the centre of the hoop. Assume that x0<R.
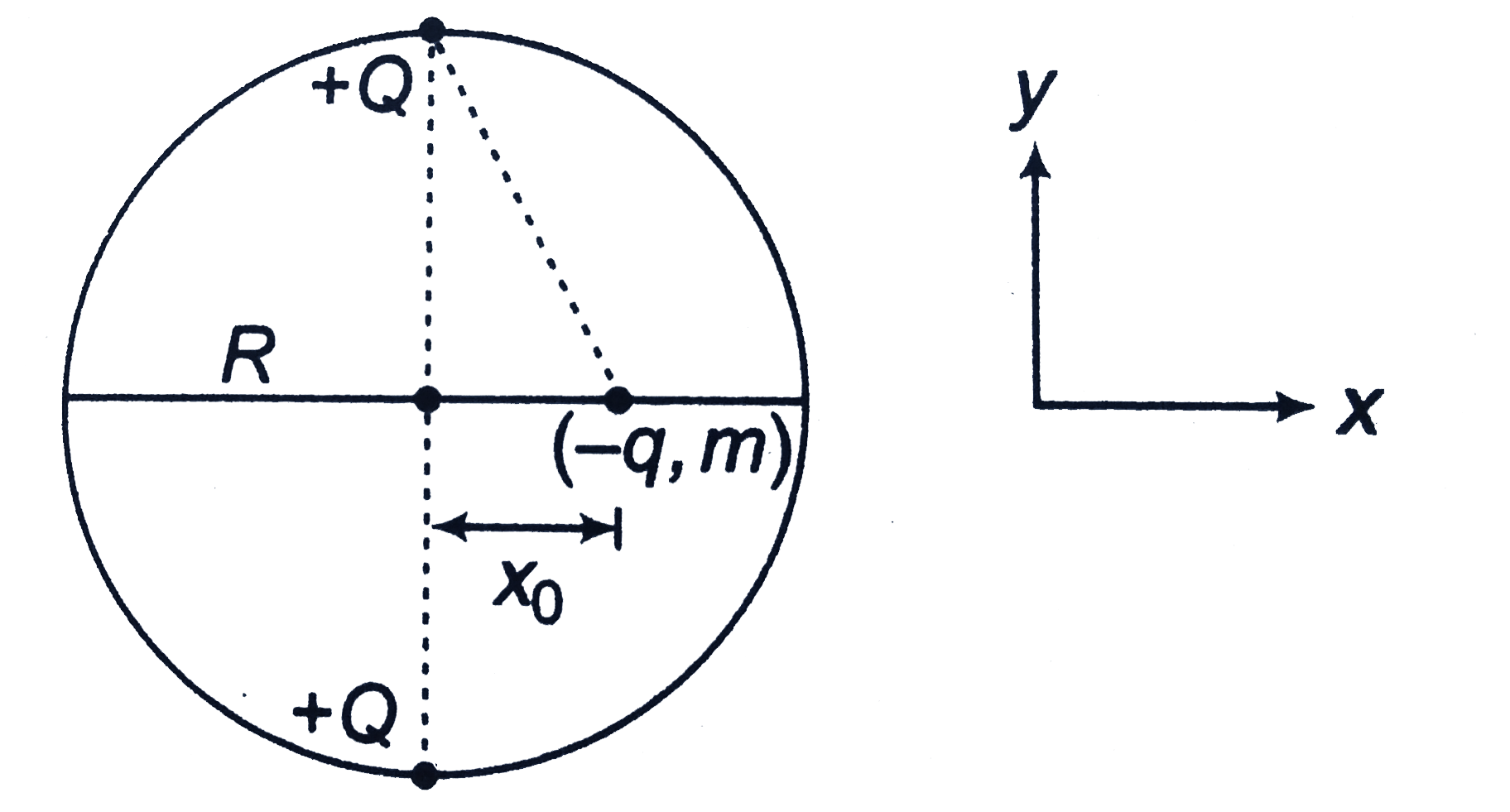
a. What is the resultant acting on the charged bead?
b. Describe (qualitatively) the motion of the bead after it is released.
c. Use the assumption that x/R<<1 to obtain an approximate equation of motion and find the displacement ad velocity of the bead as functions of time.
d. When will the velocity of the bead will become zero for the first time?
The correct Answer is:A, B, C, D
a. Fnet=2Fcosθ
=2kQ.q√R2+x202.x0√(R2+x20)(Here,k=14πε0
=2kQqx0(R2+x20)32
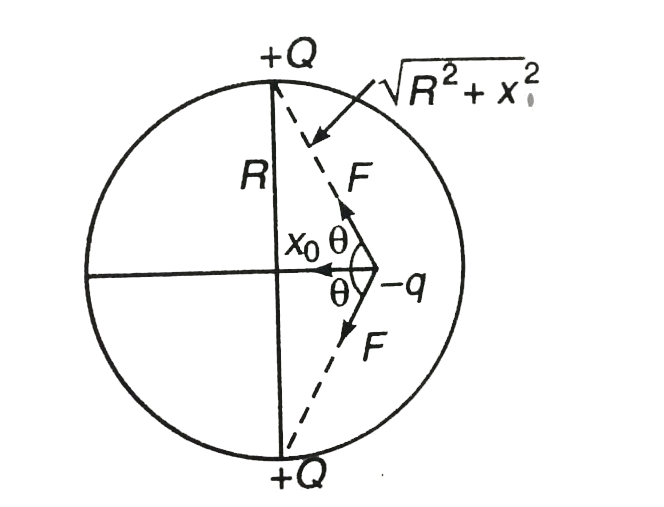
We can generalised the force by putting x0=x we have
F=−2kQqx(R2+x2)32
Motion of bead will be periodic between
x=±x0
c. for x/Rltlt1, R^2+x^2=R^2<br>or F=-((2kQq)/R^3)xor a=F/m=-((2kQq)/(mR^3))x<br>sinceaprop-xmotionwillbesimp≤ha.rmonic∈nature.<br>Compar∈gwitha=-omea^2x, omega=sqrt((2kQq)/(mR^3))<br>x=x_0cos omegat(asthepartic≤⋆tsformextremeposition)<br>v=(dx)/(dt)=-omegax_0sinomegat<br>d.Velociytwilbecomezeroatt=T/2=pi/omega<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_VOL_4_C24_E01_214_S02.pngwh=80%mx-autosty≤=background:white;><br>ort=pisqrt((mR^3)/(2kQq))
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.1
10 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.2
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Level 1 Subjective
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A thin insulating wire is stretched along the diameter of an insulated circular hoop of radius E. A small bead of mass m and charge –q is threaded onto the wire. Two small identical charge= are tied to the hoop at points opposite to each other, so that the diameter passing throughtheL-is perpendicular to the thread (see figure). The bead is released at a point which is a distance-, from the centre of the hoop. Assume that x0<<R.

a. What is the resultant acting on the charged bead?
b. Describe (qualitatively) the motion of the bead after it is released.
c. Use the assumption that x/R<<1 to obtain an approximate equation of motinand find the dislacemet ad velocity of the bead as functuions of time.
d. When will the velocity of the bead will become zero for the first time?
View SolutionA thin insulating wire is stretched·along the diameter of an. insulated circular hoop of radius R. A small bead of mass m and charge-q is threaded onto the wire. Two small identical charges are tied to the hoop at points opposite to each other, so that the diameter passing through them is perpendicular to the thread as shown in figure. The bead is released at a point which.is located at a distance x0 from the centre of the hoop. Assume that x0<<R.
(a) What is the resultant force acting on the charged bead?
(b) Describe the motion of the bead after it is released X
(c) Use the assumption that xR<<1 to obtain an approximate equation of motion, and find the displacement and velocity of the bead as functions of time
(d) When will the velocity of the bead will bcome zero for the first time?

View Solution
Knowledge Check
A circular wire of radius 2.5 cm is cut and bent to as to lie along the circumference of a hoop whose radius is 1.29 m. Find (in degrees) the angles which is subtended at the centre of the loop :
A9.67∘B7.69∘C6.97∘Dnone of these
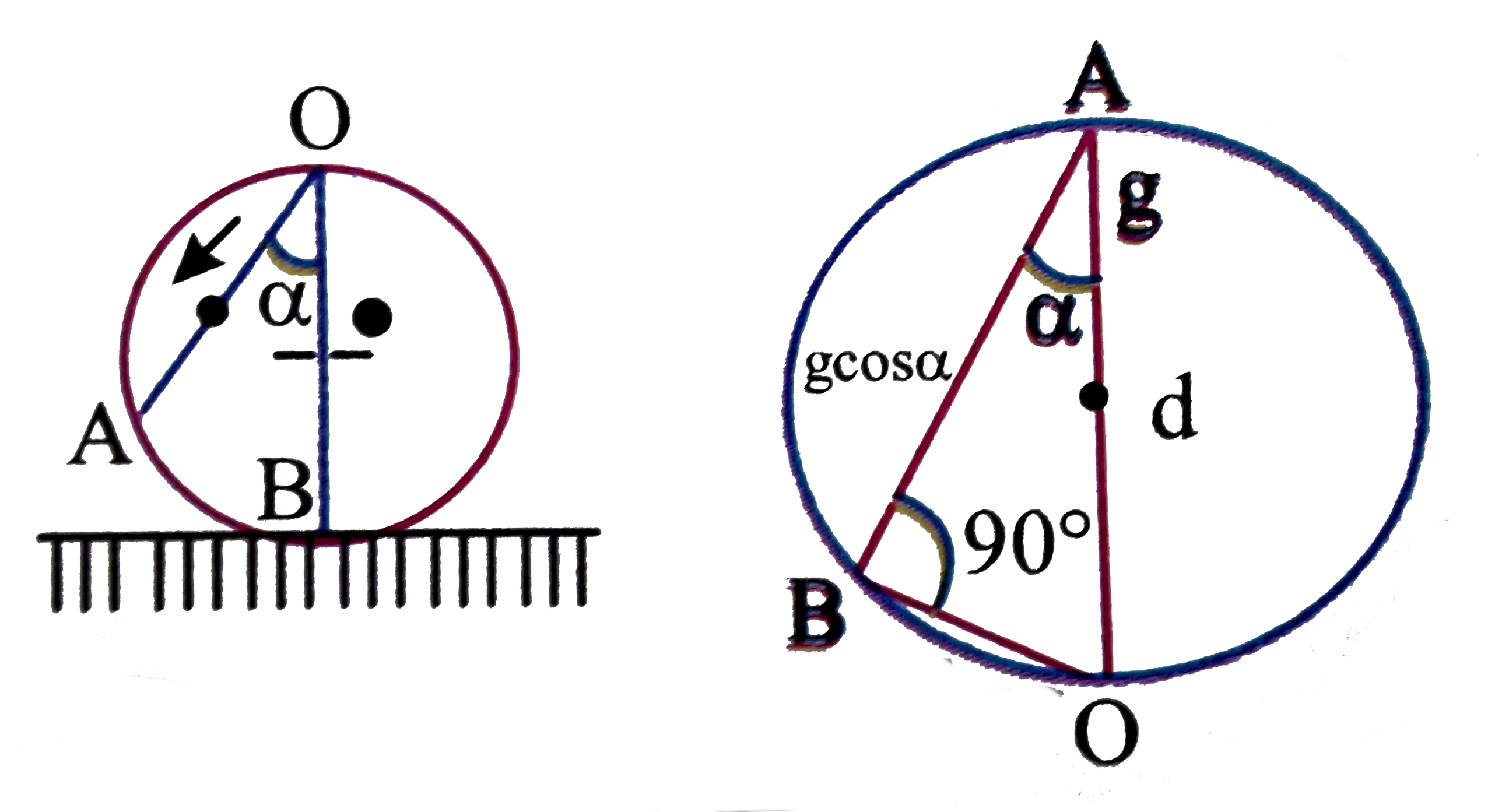
A frictionless wire is fixed between A and B inside a circle of radius R. A small bead slips along the wire. Find the time taken by the bead to slip from A to B.
View Solution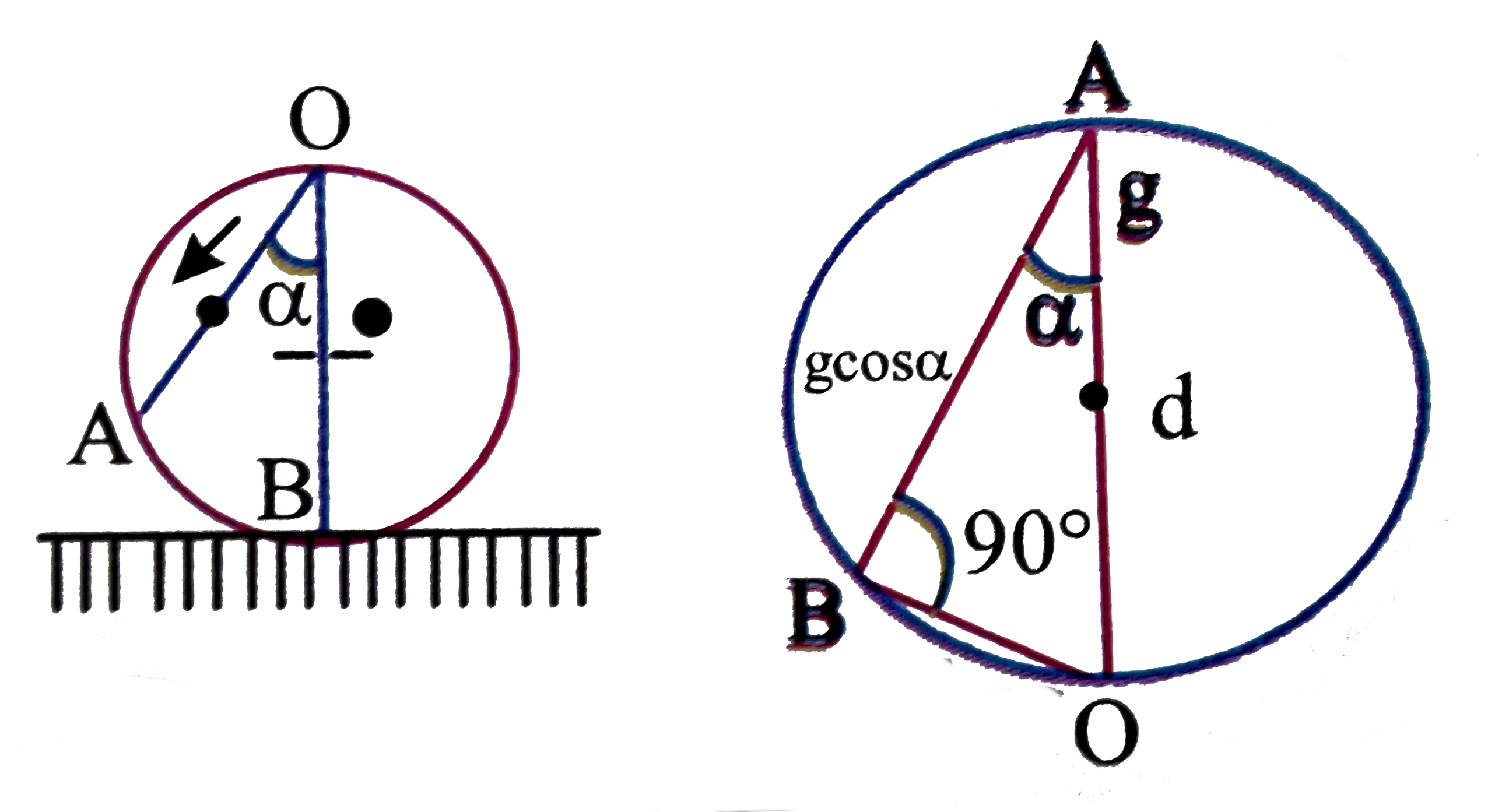
A frictionless wire is fixed between A and B inside a circle of radius R. A small bead slips along the wire. Find the time taken by the bead to slip from A to B.
View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionA thin wire ring of radius r has an electric charge q. What is the tension of the wire if a point charge q0 is placed at the ring's centre?
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View SolutionA point charge Q is placed at the centre of a circular wire of radius R having charge q. Find the force of electrostatic interaction between point charge and the wire.
View Solution
