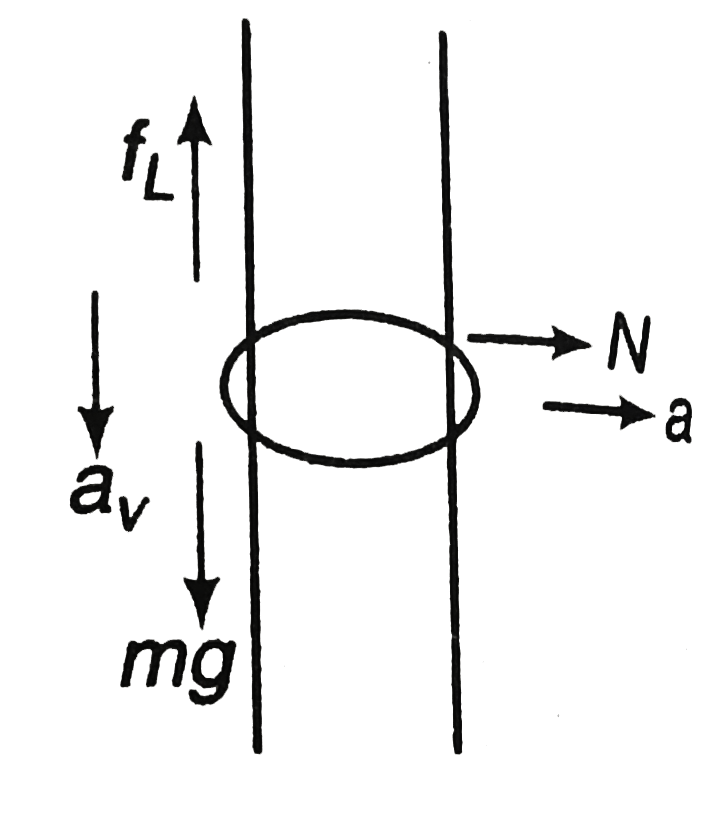
A thin rod of length 1m is fixed in a vertical position inside a train, which is moving horizentally with constant acceleration 4ms−2.A bead can slide on the rod and friction coefficient between them is 0.5. If the head is released from rest at the top of the rod , it will reach the bottom the in
√2s
1s
2s
0.5s
The correct Answer is:D
N=ma
fL=μN=0.5ma
Vertical acceleration,
aν=mg−fLm=g−0.5a
=10−0.5×4
=8m/s2
Applying s=12at2
or t=√2sa in vertical direction ,we have
t=√2×18=0.5s
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Single Correct
90 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
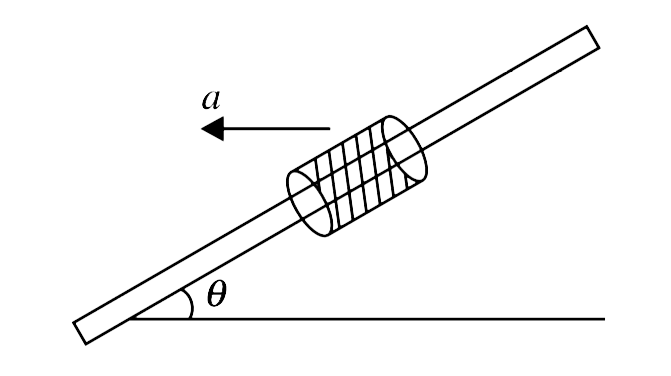
A rod is kept inclined at an angle θ with the horizontal A sleeve of mass m can slide on the rod. If the coefficient of friction between the rod and the sleeve is μ, for what values of horizontal acceleration a of the rod, towards left, the sleeve will not slide over the rod?
View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
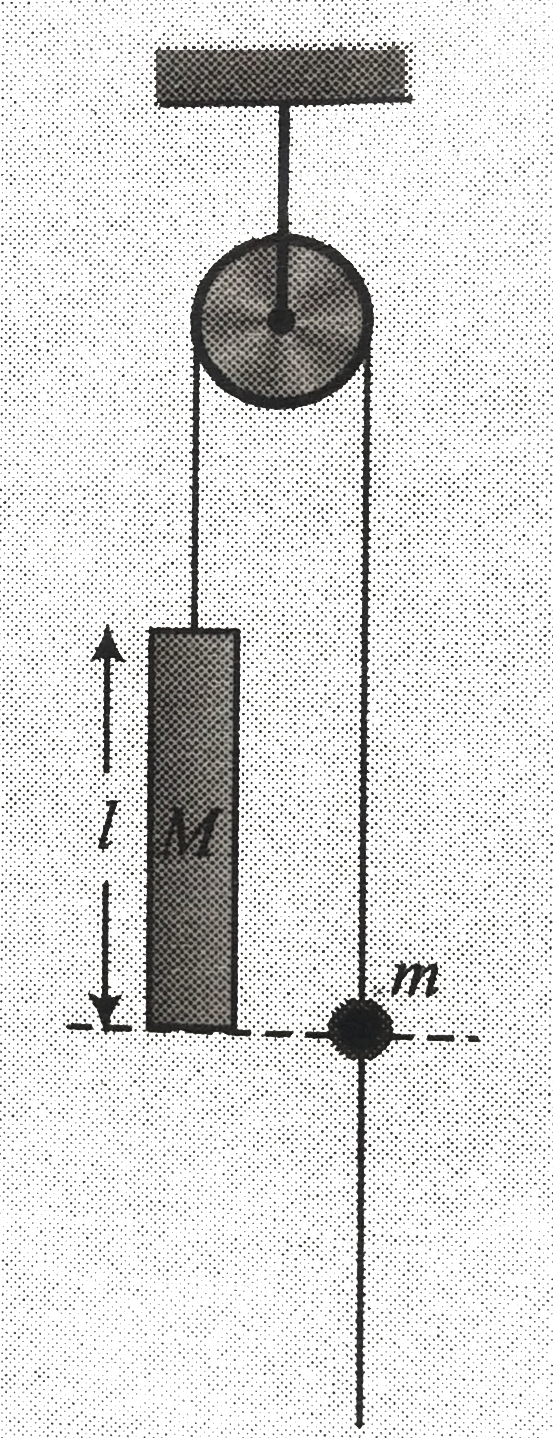
View Solution
Knowledge Check
A long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isA B
B C
C D
D
A long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isA√μ/αBμ/√αC1√μαDinfinitesimalA long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isA√μαBμ√αC1√μαDInfinitesimal
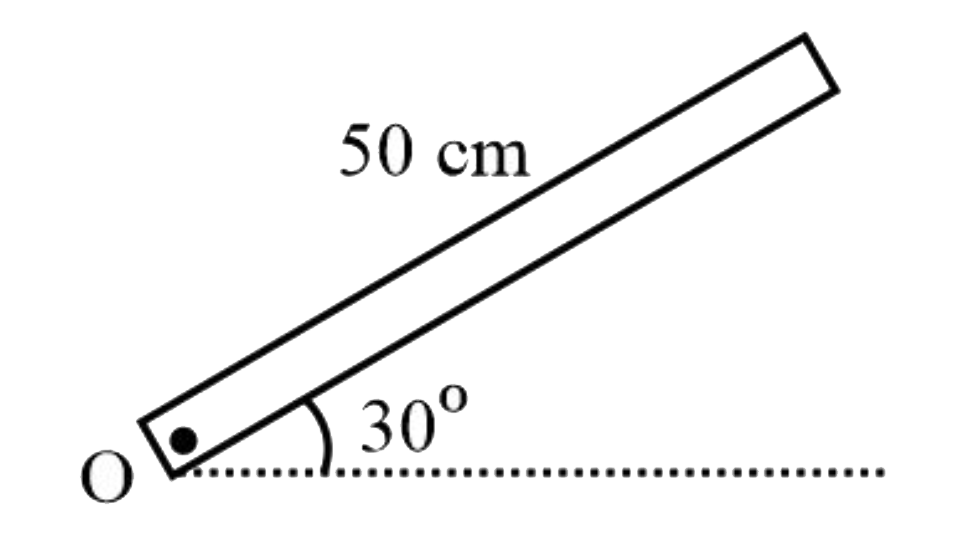
A uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA uniform rod of mass M and length L is hinged at its lower end so as to rotate freely in the vertical plane of the fig. There is a small tight fitting the hinged end. A small mass less pin welded to the rod supports the bead. The system is released from the vertical position shown. It was observed that the bead just begins to slide on the rod when the rod becomes horizontal.
(a) Find the normal contact force between the rod and the bead when the rod gets horizontal. What is the direction of this force?
(b) Find the coefficient of friction between the bead and rod.

View SolutionA long horizontal rod has a bead which can slide along its length and is initially placed at a distance L from one end A of the rod. The rod is set in angular motion about A with a constant angular acceleration, α. If the coefficient of friction between the rod and bead is μ, and gravity is neglected, then the time after which the bead starts slipping is :
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View Solution
