A transparent solid cylindrical rod has a refractive index of 2√3. It is surrounded by air. A light ray is incident at the midpoint of one end of the rod as shown in Fig 2.31. Determine the incident angle θ for which the light ray grazes along the wall of the rod.

For refraction of light at point B, we can write by applying Snell.s law,
1×sinθ=μsinr
[where mu is the refractive index of the solid material]
or, sinθ=2√3sinr
The light ray BC in incident on point C making critical angle θc and propagates along CD [Fig. 2.32.]
Thus, from Snell.s law,
μ=1sinθc
or, θc=sin−1(1μ)=sin−1(√32)=60∘
∴ r=180∘−(60∘+90∘)=30∘
Hence from equation (1), we can write
sinθ=2√3sin30∘=1√3or,θ=sin−1(1√3)

Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)
25 Videos
- REFRACTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION
18 Videos
- REFLECTION OF LIGHTBOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE
3 Videos
- SEMICONDUCTORS AND ELECTRONICS BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER
31 Videos
Similar Questions
A transparent solid cylindrical rod has a refractive index of 2√3 .It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure. The incident angle θ for which the light ray grazes along the wall of the rod is:
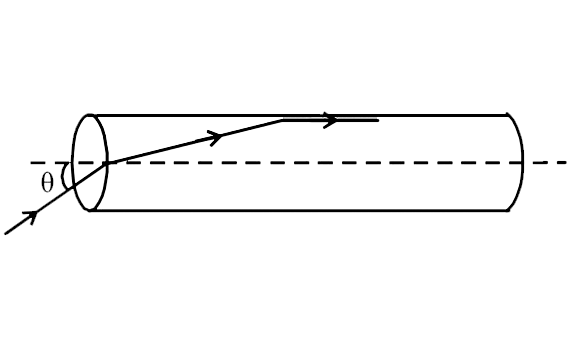
View SolutionA transparent solid cylinderical rod has a refractive index of 2√3. It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure. The incident angle θ for which the light ray grazes along the wall of the rod is

View Solution
Knowledge Check
A transparent solid cylindrical rod has a refractive index of 2√3 .It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure. The incident angle θ for which the light ray grazes along the wall of the rod is:
 Asin−1(√32)Bsin−1(2√3)Csin−1(1√3)Dsin−1(12)
Asin−1(√32)Bsin−1(2√3)Csin−1(1√3)Dsin−1(12)A transparent solid cylinder rod has a refractive index of 2√3. It is surrounded by air. A light ray is incident at the mid point of one end of the rod as shown in the figure.
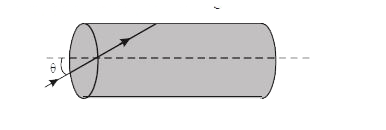
The incident angle θ for which the light ray grazes along the wall of the rod isAsin−1(12)Bsin−1(√32)Csin−1(2√3)Dsin−1(1√3)Light ray is incident on a prism of angle A=60∘and refractive indexμ=√2.the angle of incidence at which the emergent ray grazes the surface is given by
Asin−1(√3−12)Bsin−1(1−√32)Csin−1(√32)Dsin−1(2√3)
A transparent solid cylinder rod has a refractive index of 2√3It is surrounded by air. A light ray is incident at the mid point of one end of the rod as shown in the figure.
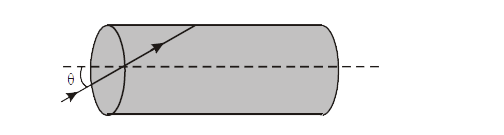
The incident angle θ for which the light ray grazes along the wall of the rod is
View SolutionLight incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.
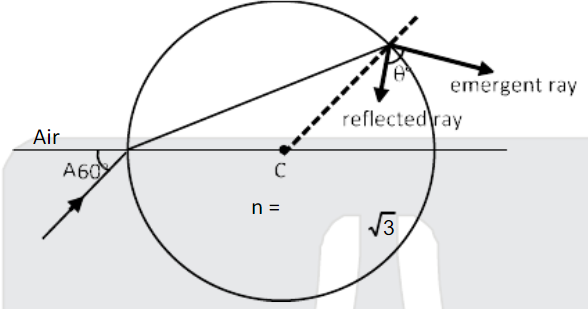
View SolutionLight incidence on a sphere of refractive index √3 placed in a air as shown in Figure. Find the angle (θ)in degree between emergent ray and reflected ray.

View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View Solution
