A tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
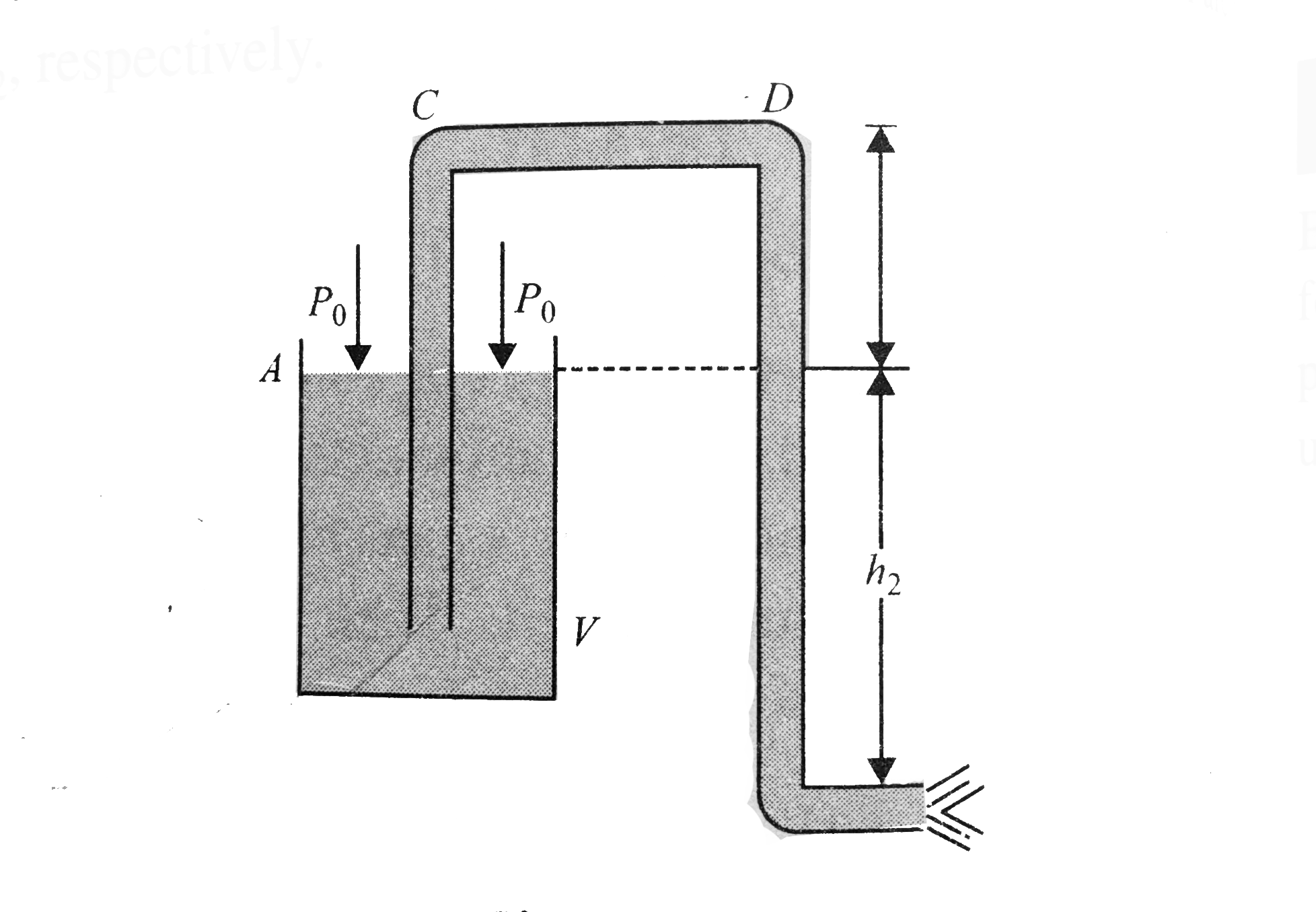
If h1=h2=3.0m, the maximum value of h1, for which the siphon will work will be
3.0m
6.0m
7.2m
4.8m
The correct Answer is:C
We apply Bernoulli's theorem for level A and for the highest level, CD (labelled by subscript 1) to get
PA=P1+12ρv21+ρgh1…….i
Since the tune has uniform cross section and water is incompressible
v1=vB=√2gh2………..ii
From eqn i and
P1=PA−12ρ[√2gh2]2−ρgh1
=Patm−ρg(h1+h2)...........iii
The minimum value of P1=0(P1 cannot be negatie because then no water will reach the level). Hence putting P1=0.
(h1)max=Patmρg−h2=1.0×1051×103×9.8−3.0
=10.2m−3.0m=7.2m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - True/False1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE13videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning8videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
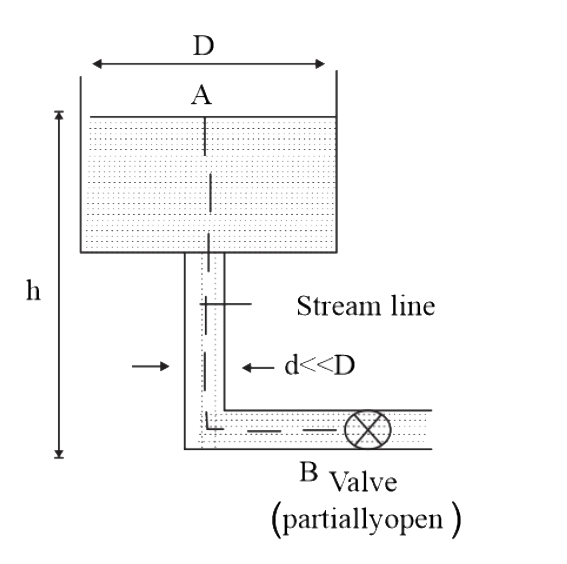
The bottom of a cylindrical vessel has a circlular hole of radius r and at depth h below the water] level. If the diameter of the vessel is D, the find then speed with which the water level in the] vessel drops.
View SolutionA U-tube of uniform cross-sectional area and open to the atmosphere is partially filled with mercury. Water is then poured into both arms. If the equilibrium configuration of the tube is as shown in figure with h2=1.0cm, determine the value of h1
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
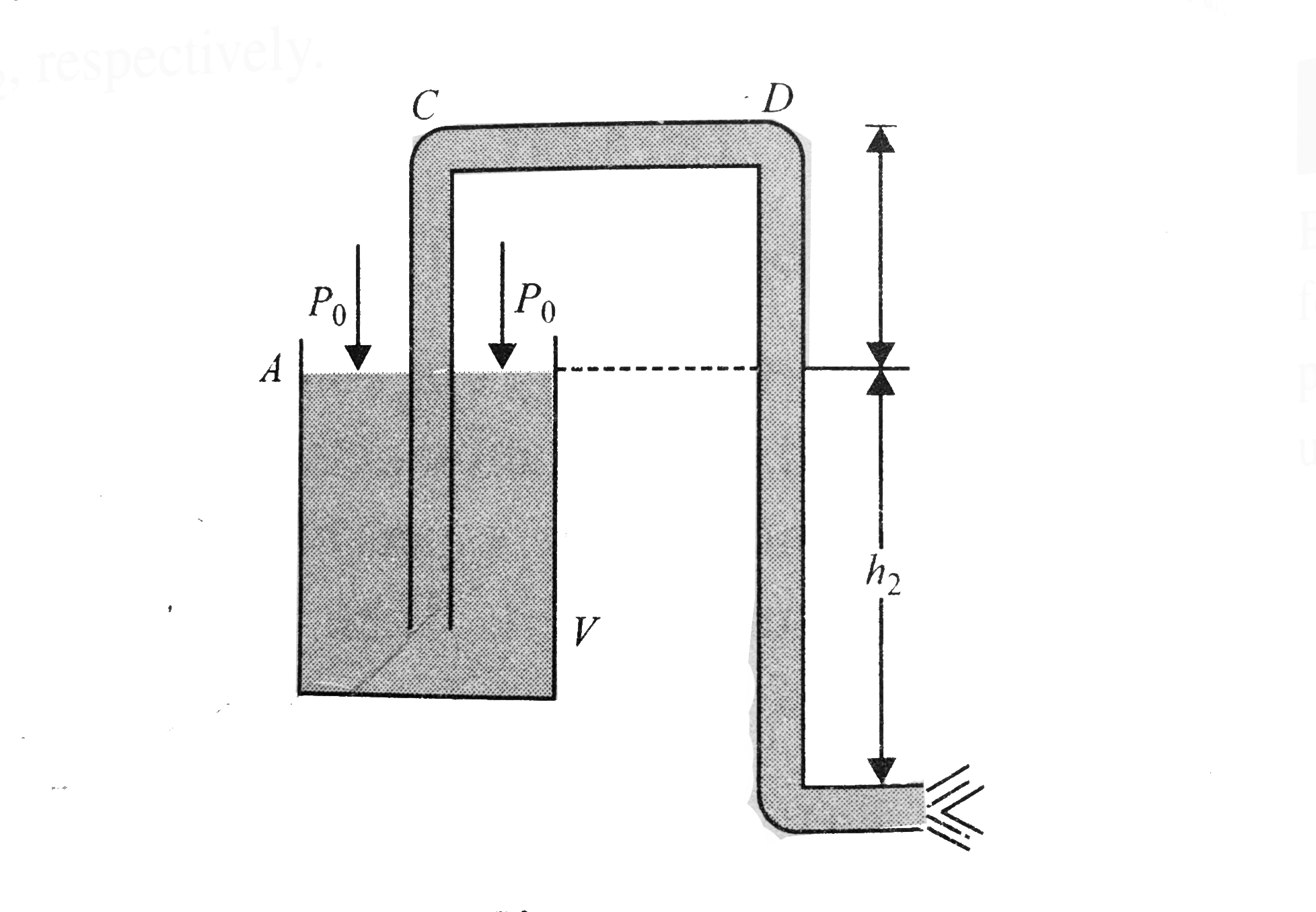
Given h1=h2=3.0m, the gauge pressure of water in the highest level CD of the tube will beA3.0×104N/m2B5.9×104N/m2C5.9×104N/m2D1.5×104N/m2 - Question 2 - Select One
A tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.

Determine the velocity vB of the water issuing out at B.AvB=√2gh2BvB=√2h(h1+h2)CvB=√2h(h2−h1)DvB=√gh2 - Question 3 - Select One
A tube of small uniform cross section is used to siphon the water from the vessel. Then choose the correct alternative (s) :
(ρwater=103kg/m3,g=10m/s2,Patm=105Pa)
 AWater will come out from section B with a velocity of √80m/sBThe greatest value of h1 for which the siphon will work is 10 m.Cboth are correctDboth are wrong
AWater will come out from section B with a velocity of √80m/sBThe greatest value of h1 for which the siphon will work is 10 m.Cboth are correctDboth are wrong
To measure the atmospheric pressure, four different tubes of length 1m, 2m , 3m and 4m are used. If the height of the mercury column in the tubes is h1,h2,h3,h4 respectively in the four cases, then h1:h2:h3:h4
View SolutionA bent tube is lowered into the stream as shown in the figure below. The velocity of the stream relative to the tube equal to v. The closed upper end of the tube located at the light h0. To what height h will the water jet spurt ?
 View Solution
View SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
 View Solution
View SolutionThe height of water in a vessel is h. The vessel wall of width b is at an angle θ to the vertical. The net force exerted by the water on the wall is
 View Solution
View SolutionIf atmosphere pressure at a height of h units is given by the function P(h)=he−h then pressure is maximum at the height of
View Solution

