A uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
43R
√172R
√13R
√152R
The correct Answer is:B
To solve the problem of finding the distance d such that the moment of inertia of a uniform disc about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, we can follow these steps:
Step 1: Calculate the Moment of Inertia I1 about the axis x=2R and y=0
Using the parallel axis theorem, the moment of inertia about an axis parallel to the one through the center of mass is given by:
I1=Icm+Mh2
Where:
- Icm is the moment of inertia about the center of mass,
- M is the mass of the disc,
- h is the distance from the center of mass to the new axis.
For a uniform disc, the moment of inertia about its center is:
Icm=12MR2
The distance h from the center of the disc (at the origin) to the axis x=2R is 2R. Thus:
I1=12MR2+M(2R)2=12MR2+4MR2=12MR2+8MR2=92MR2
Step 2: Calculate the Moment of Inertia I2 about the axis y=d and z=0
Again using the parallel axis theorem, we can express I2:
I2=Icm+Md2
For the axis through the center of mass (diameter), the moment of inertia is:
Icm=14MR2
Thus, we have:
I2=14MR2+Md2
Step 3: Set I1 equal to I2
According to the problem, we have:
I1=I2
Substituting the expressions we derived:
92MR2=14MR2+Md2
Step 4: Simplify the Equation
We can cancel M from both sides (assuming M≠0):
92R2=14R2+d2
Now, we can rearrange this:
d2=92R2−14R2
Finding a common denominator (which is 4):
d2=184R2−14R2=174R2
Step 5: Solve for d
Taking the square root of both sides:
d=√174R2=√172R
Final Answer
Thus, the value of d is:
d=√172R
---
- Icm is the moment of inertia about the center of mass,
- M is the mass of the disc,
- h is the distance from the center of mass to the new axis.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
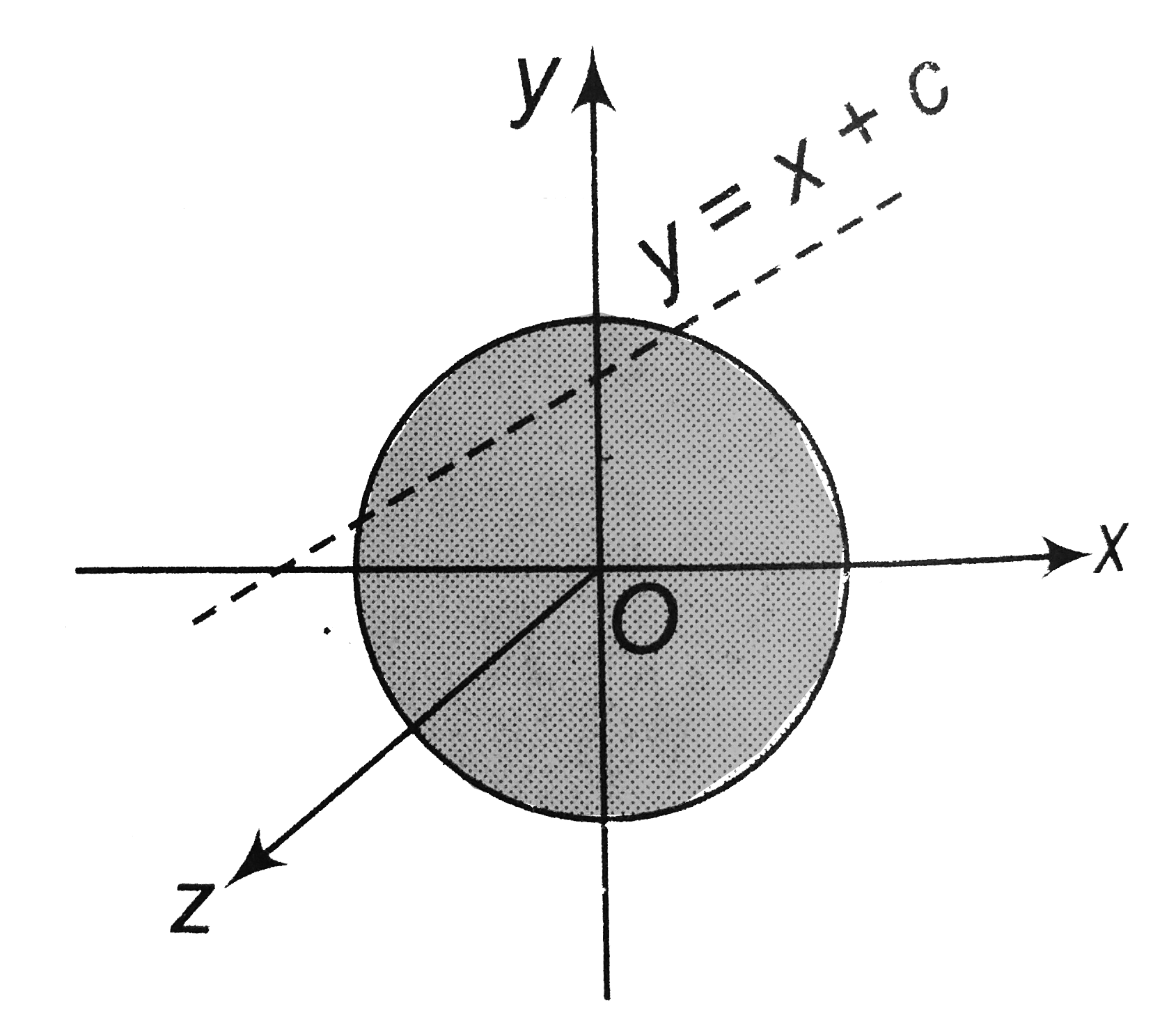
A uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
 .
.
View SolutionA rod is placed along the line,y=2x with its centre at origin. The moment of inertia of the rod is maximum about.
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionA square plate lies in the xy plane with its centre at the origin and its edges parallel to the x and y axes. Its moments of inertia about the x, y and z axes are Ix,Iy and IZ respectively, and about a diagonal it is ID
View SolutionA circular disc of radius R and thickness R6 has moment of inertia I about its axis. If it is melted and casted into a solid sphere then what will be its moment of inertia, about its diametric axis?
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is

View SolutionFour identical rods, each of mass m and length l, make a square frame in the xy plane as shown in Fig.
a. Calculate its moment of inertia about the x-and y-axes.
b. Also, calculate its moment of inertia about the z-axis.

View SolutionThe surface density (mass/area) of a circular disc of radius a depends on the distance from the centre as ρ(r)=A+Br. Find its moment of inertia about the line perpendicular to the plane of the disc through its centre.
View SolutionThe surface density (mass/area) of a circular disc of radius a depends on the distance from the centre as ρ(r)=A+Br. Find its moment of inertia about the line perpendicular to the plane of the disc through its centre.
View SolutionFigure shows a body of arbitrary shape 'O is the centre of mass of the body and mass of the body is M. If moment of inertia about axis CC is Icc'. then moment of inertia about axis AA' (I AA')will be equal to
View Solution
