A uniform electric field exists in space. Find the electric flux of th

A cone lies in a uniform electric field $E$ as shown in figure. The electric flux entering the cone is

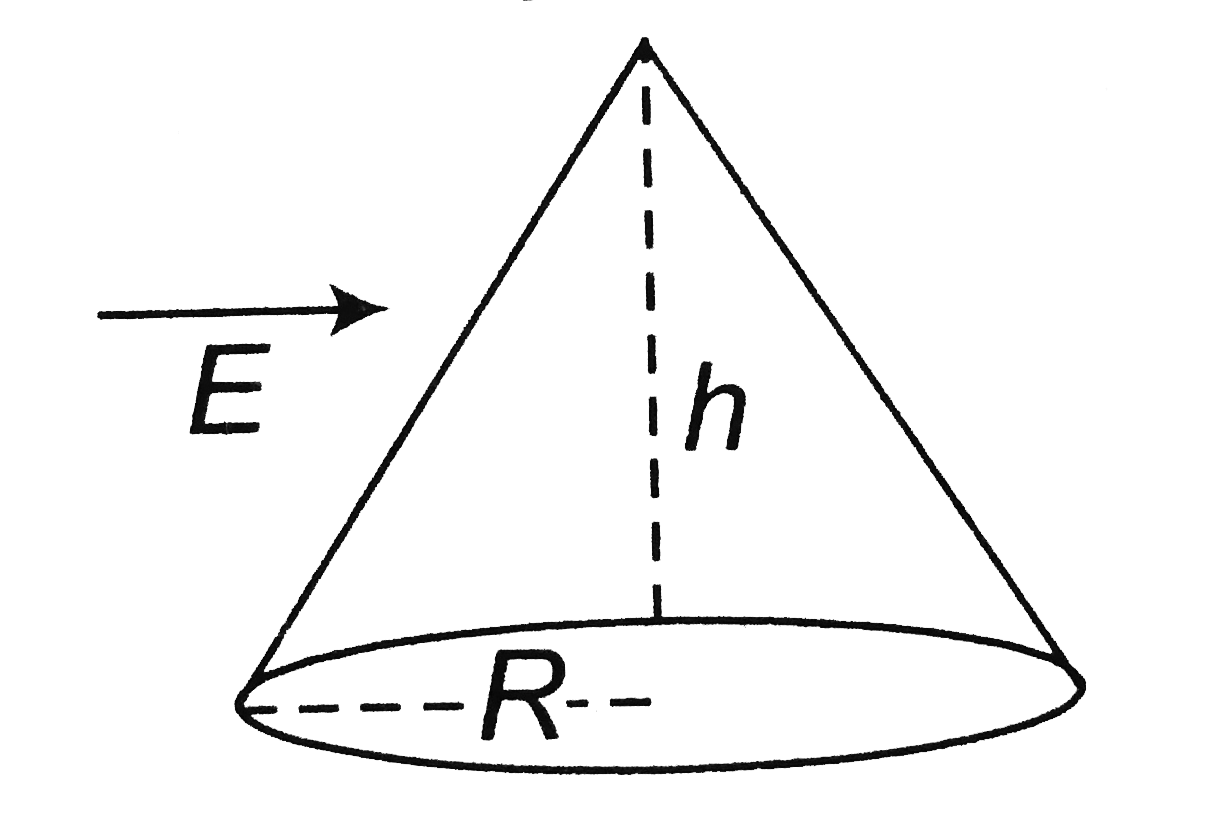A $E π R^{2}$
B $E R h$
C $\frac{E h R}{2}$
D $E h^{2}$
The flux of electric field due to these charges through the surface S is

A $\frac{2 q}{ε_{0}}$
B $\frac{3 q}{ε_{0}}$
C $\frac{- 5 q}{ε_{0}}$
D $q ε_{0}$
A hemispherical body of radius R is placed in a uniform electric field E. What is the flux linked with the curved surface if, the field is (a) parallel to the base, (b) perpendicular to the base.
A $ϕ = (E (π R)$
B $ϕ = (E S = E (π R^{3})$
C $ϕ = E (π R^{2})$
D $ϕ = (E S = E (π R^{4})$

A uniform electric field exists in space. Find the electric flux of the filed thourgh curved surface area of the cyclinder with its axis paralel to the field.