A uniform rod AB of mass m and length 2a is falling freely without rotation under gravity with AB horizontal. Suddenly the end A is fixed when the speed of the rod is v. The angular speed which the rod begains to rotate is
v2a
4v3a
v3a
3v4a
The correct Answer is:D
To solve the problem, we will use the principle of conservation of angular momentum. Here’s a step-by-step solution:
Step 1: Understand the System
We have a uniform rod AB of mass m and length 2a that is falling freely under gravity with its horizontal position. The end A of the rod is suddenly fixed when the rod has a speed v.
Step 2: Identify the Initial Angular Momentum
Before the end A is fixed, the rod is falling with a linear velocity v. The center of mass of the rod is at a distance a from point A (the midpoint of the rod). The initial angular momentum Li about point A can be calculated using the formula:
Li=m⋅v⋅r
where r is the distance from point A to the center of mass, which is a. Therefore, we have:
Li=m⋅v⋅a
Step 3: Identify the Final Angular Momentum
Once point A is fixed, the rod will start to rotate about point A. The moment of inertia I of the rod about point A is given by:
I=13mL2
where L=2a (the length of the rod). Thus,
I=13m(2a)2=43ma2
The final angular momentum Lf when the rod starts rotating with angular speed ω is given by:
Lf=I⋅ω=43ma2⋅ω
Step 4: Apply Conservation of Angular Momentum
According to the conservation of angular momentum:
Li=Lf
Substituting the expressions we found:
m⋅v⋅a=43ma2⋅ω
Step 5: Simplify and Solve for Angular Speed ω
We can cancel m from both sides (assuming m≠0):
v⋅a=43a2⋅ω
Now, divide both sides by a (assuming a≠0):
v=43a⋅ω
Rearranging gives:
ω=3v4a
Final Answer
Thus, the angular speed ω that the rod begins to rotate with is:
ω=3v4a
We have a uniform rod AB of mass m and length 2a that is falling freely under gravity with its horizontal position. The end A of the rod is suddenly fixed when the rod has a speed v.
Before the end A is fixed, the rod is falling with a linear velocity v. The center of mass of the rod is at a distance a from point A (the midpoint of the rod). The initial angular momentum Li about point A can be calculated using the formula:
Li=m⋅v⋅r
where r is the distance from point A to the center of mass, which is a. Therefore, we have:
Li=m⋅v⋅a
Once point A is fixed, the rod will start to rotate about point A. The moment of inertia I of the rod about point A is given by:
I=13mL2
where L=2a (the length of the rod). Thus,
I=13m(2a)2=43ma2
Lf=I⋅ω=43ma2⋅ω
According to the conservation of angular momentum:
Li=Lf
Substituting the expressions we found:
m⋅v⋅a=43ma2⋅ω
We can cancel m from both sides (assuming m≠0):
v⋅a=43a2⋅ω
Now, divide both sides by a (assuming a≠0):
v=43a⋅ω
Rearranging gives:
ω=3v4a
Thus, the angular speed ω that the rod begins to rotate with is:
ω=3v4a
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
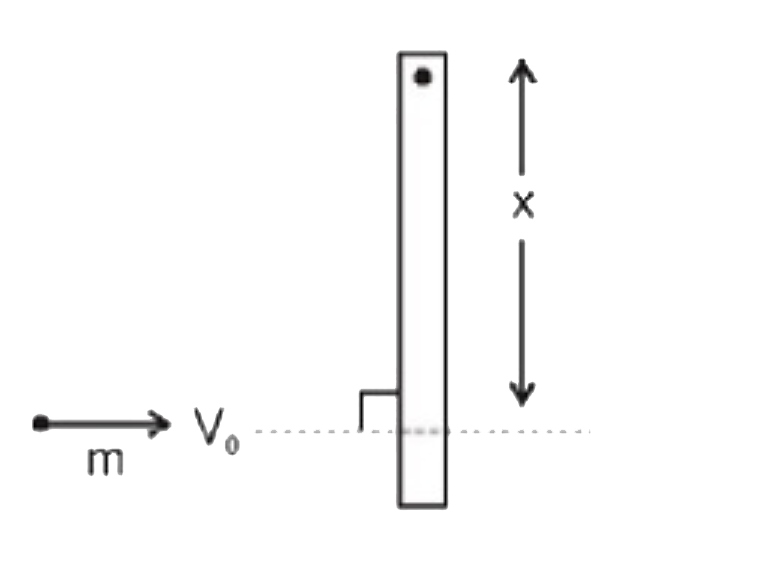
View SolutionA uniform rod of mass m and length L is hinged at one end and free to rotate in the horizontal plane. All the surface are smooth. A particle of same mass m collides with the rod with a speed V0. The coefficient of restitution for the collision is e=12. If hinge reaction during the collision is zero then the value of x is :
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View SolutionA rod of mass M and length L is falling vertically with speed v. Suddenly its one end gets stuck in a friciitonless hook. Find the angular velocity of the rod just after its end gets struck.

View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
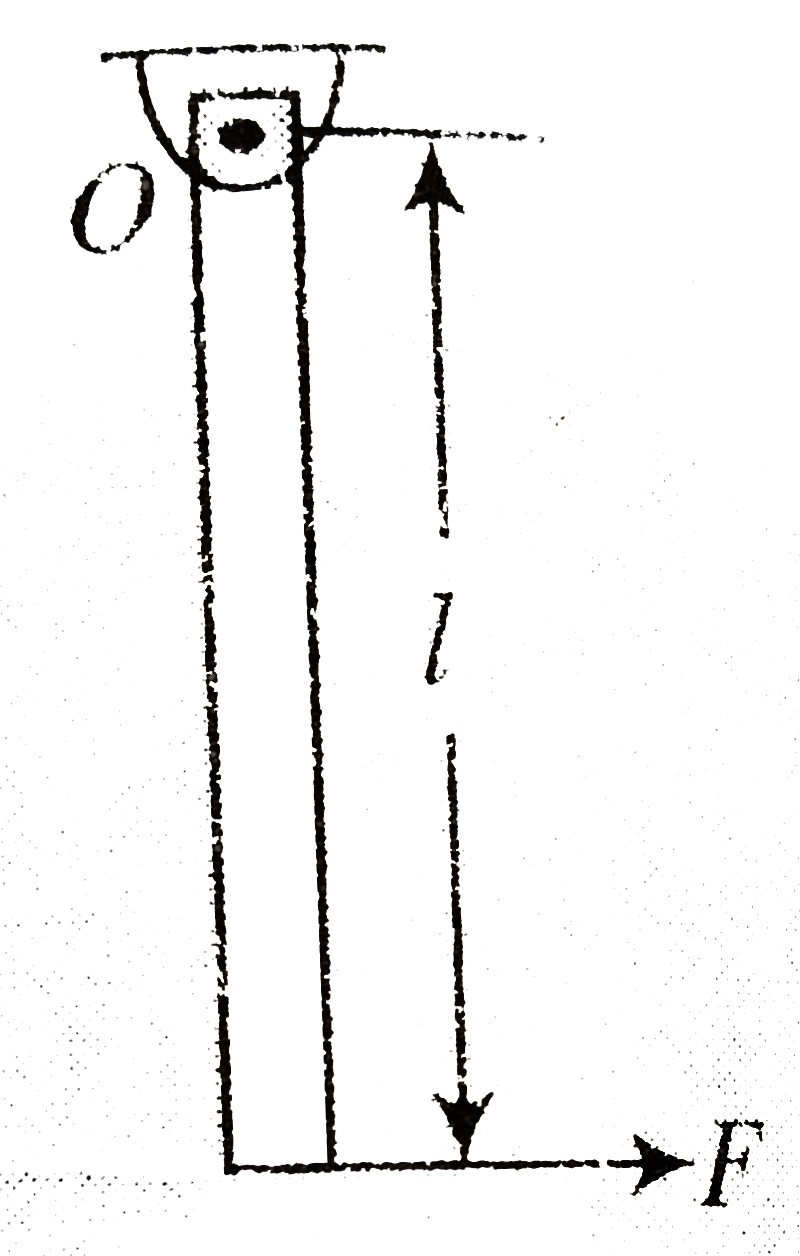
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View SolutionA uniform rod of mass m=2kg and length l is kept on a smooth horizontal plane. If the ends A and B of the rod move with speeds v and 2v respectively perpendicular to the rod, find the:
a. angulr velocity of CM of the rod.
b. Kinetic energy of the rod (in Joule).

View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
