A uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
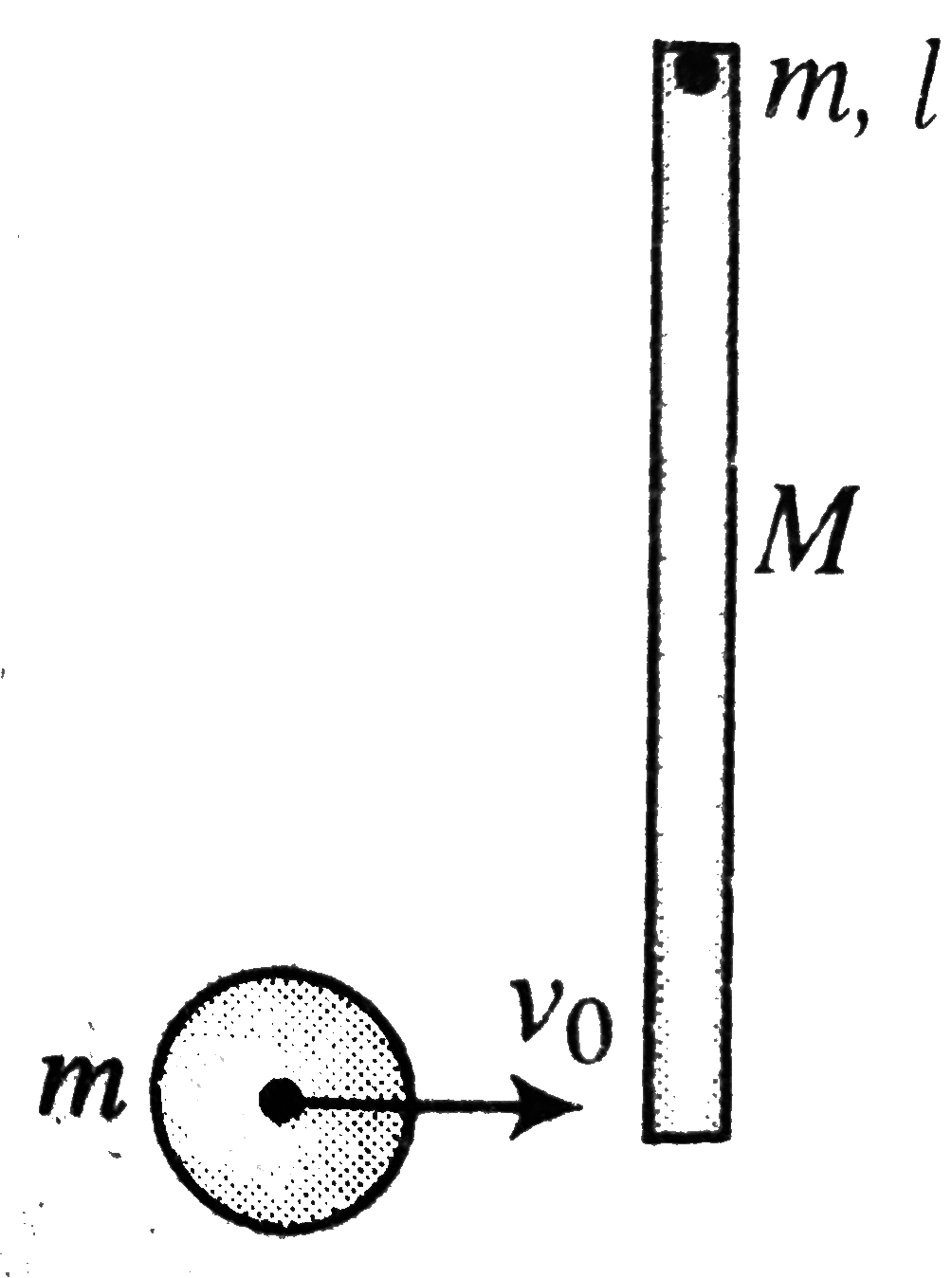
The correct Answer is:25mv0
a. Since net torque about the pivot for (ball +rod) system is zero using conservation of agular momentum
mv0l=mvl+ml23ω
v0=v+23ωl[∵M=2m] ………i
Also, for elastic collision e=1
ωl−v=v0…ii
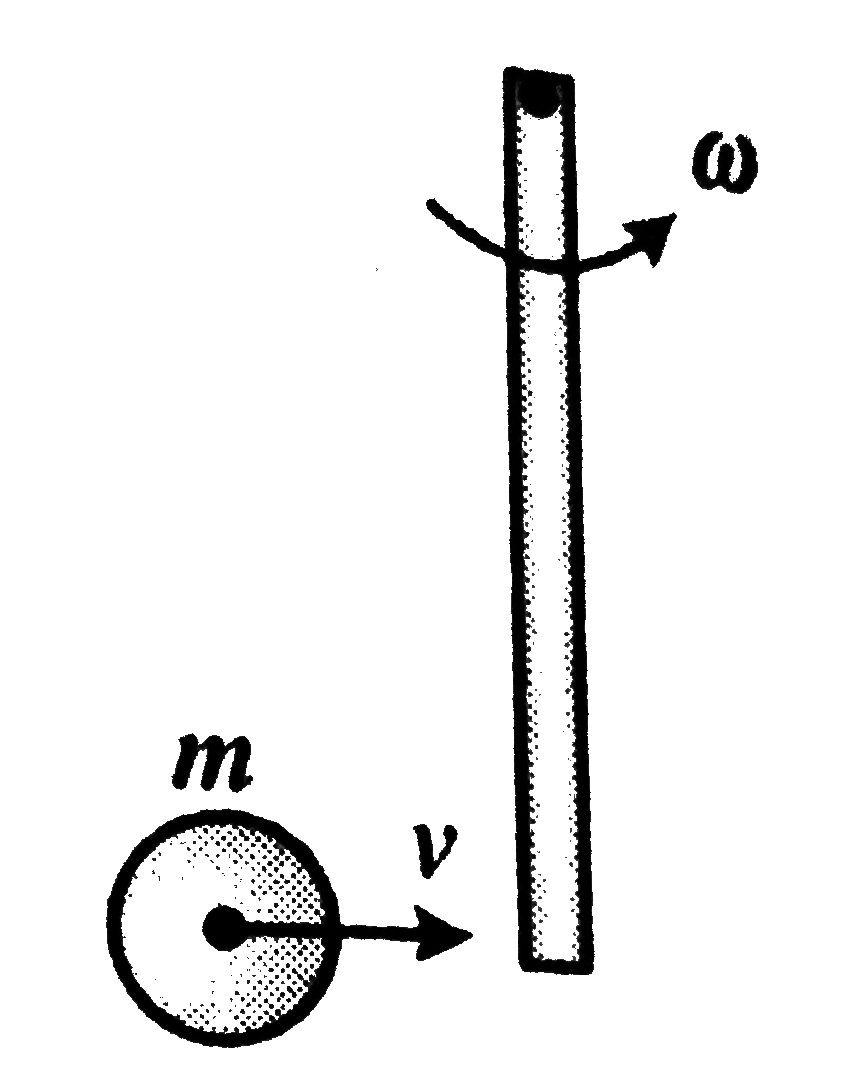
Solving eqn i and ii we get
2v0=53ωl
∴ω=6v05l
b.Now for rod, angular impulse about the pivot=change in angular momentum about the pivot
Jl=Ml2ω
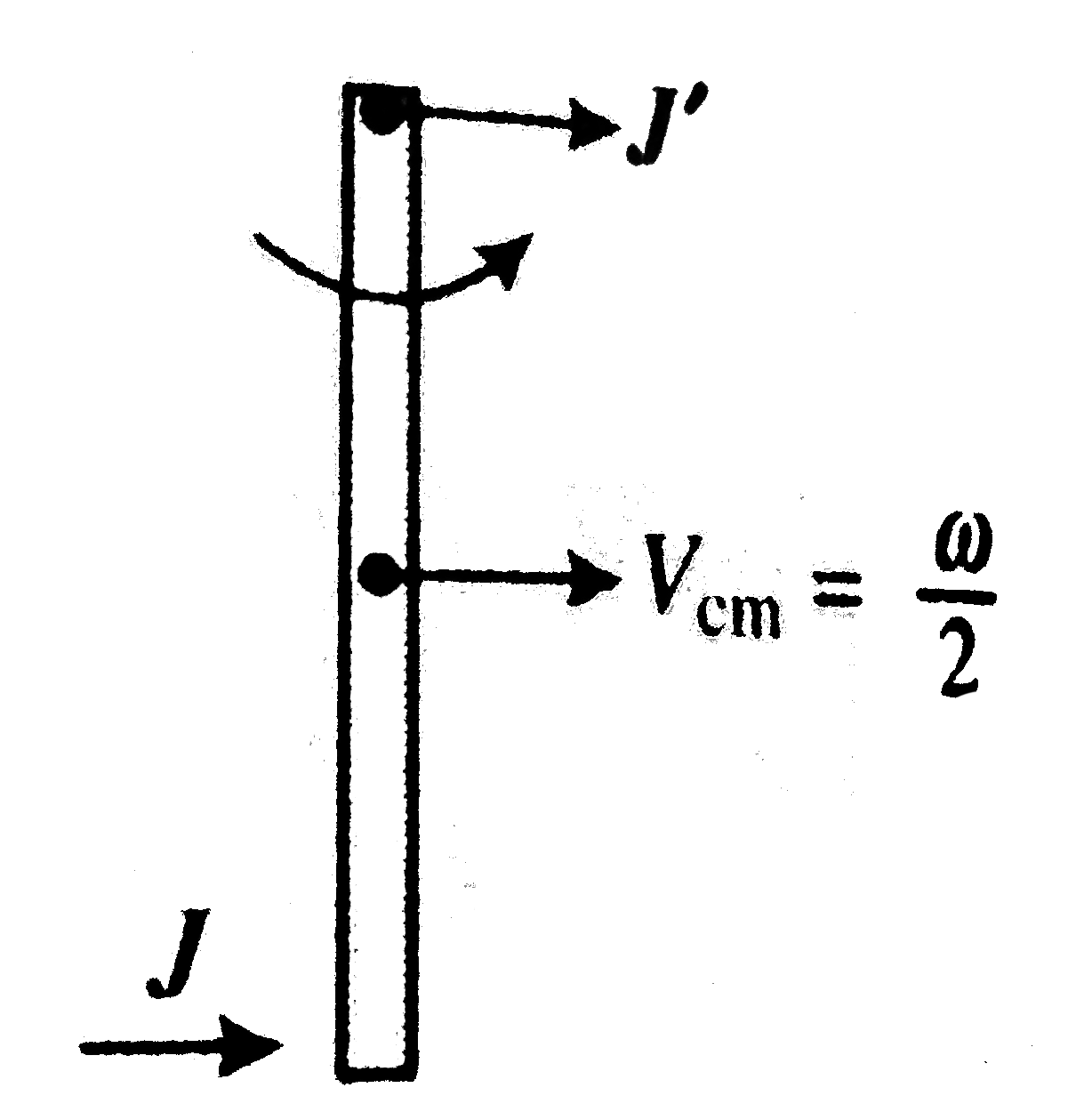
∴J=23mωl=23m×6v05=4mv05
Now using imple momentum equation for the rod
J+J'=Mωl2
⇒45mv0+J'=2mωl2⇒45mv0+J'=65mv0
∴J'=25mv0
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
 View Solution
View SolutionA rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v0 hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A(2πmlpB(2π)(pmlCπml12pDπpml - Question 2 - Select One
A uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 A6v05LB12v05LC2v05LD3v07L
A6v05LB12v05LC2v05LD3v07L - Question 3 - Select One
A uniform rod AB of mass m and length l at rest on a smooth horizontal surface. An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 A2πmlPBπml3PCπml12PD2πml3P
A2πmlPBπml3PCπml12PD2πml3P
A rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision the particle comes to rest. Find the ration m/M.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 View Solution
View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

Distance travelled by the centre of the rod, while rod rotates by 90∘View SolutionA uniform rod of mass M and length L is moving on a smooth horizontal plane, such that its one end is moving with a velocity V0 and other end is moving with velocity 2V0 in the same direction as shown. Then which of the following is kinetic energy of the rod?
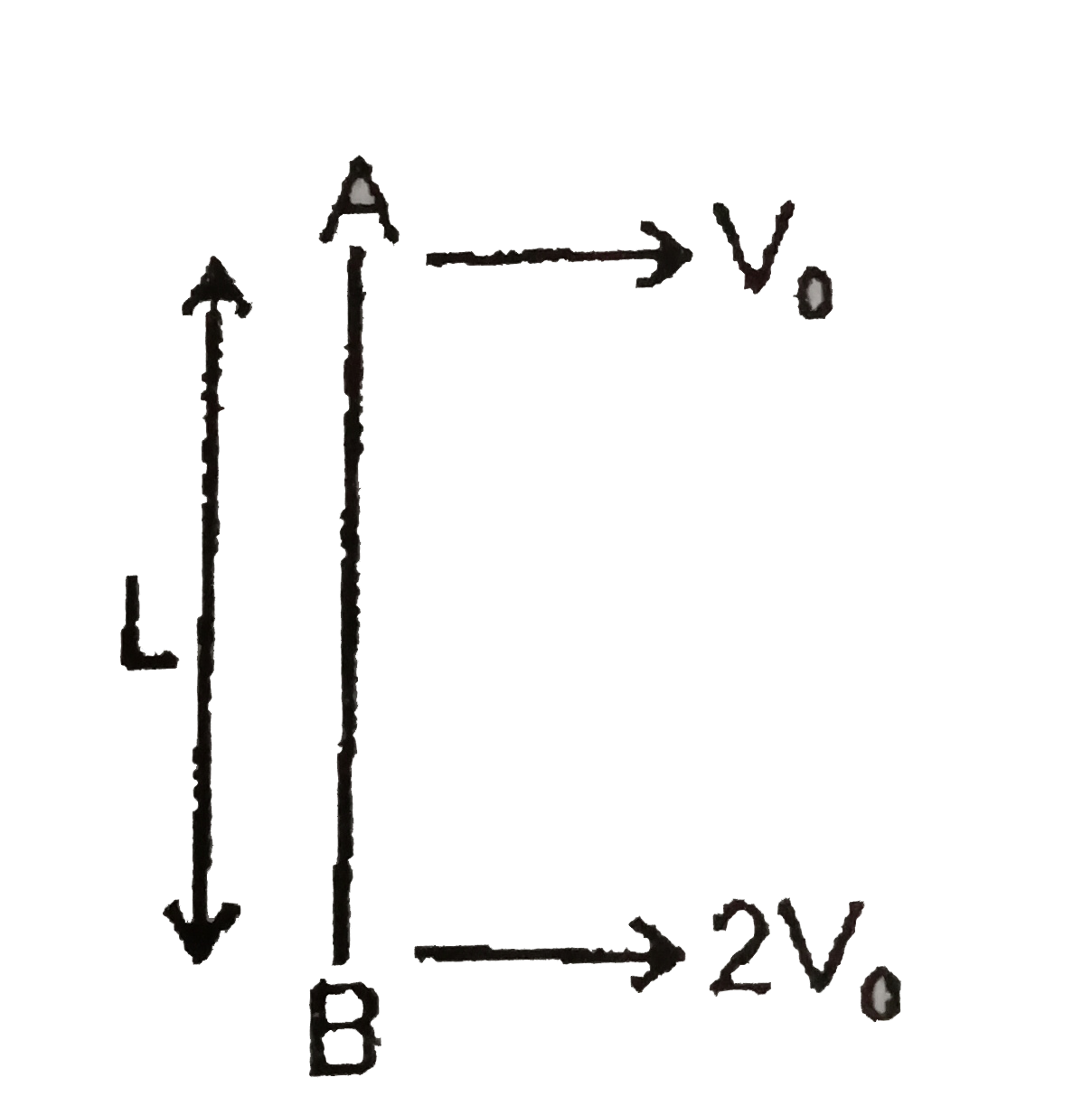 View Solution
View Solution

