A uniform rod of weight and length is supported at its ends by a frictionless through as shown in figure. (a) Show that the centre of gravity of the rod must be vertically over point when the rod is in equilibrium. (b) Determine the equilibrium value of the angle .

a. Just three forces act on the rod forces perpendicular to the sides of the through at and , and its weight. The lines of action of and will intersect at a point above the rod. They will have no torque about this point. The rod's weight will cause a torque about the point of intersection as in figure a. and the rod will not be equlibrium unles the centre of the rod lies vertically below the intersection point as is shown in figure b.

All three forces must be concurrent. Then the line of action of the weight is a diagonal of the rectangle formed by the through and the normal forces, and the rod's centre of gravity is vertically above the bottom of the trough.
b. In figure b,
so and
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.411videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.217videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
Knowledge Check
- Question 1 - Select One
A thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
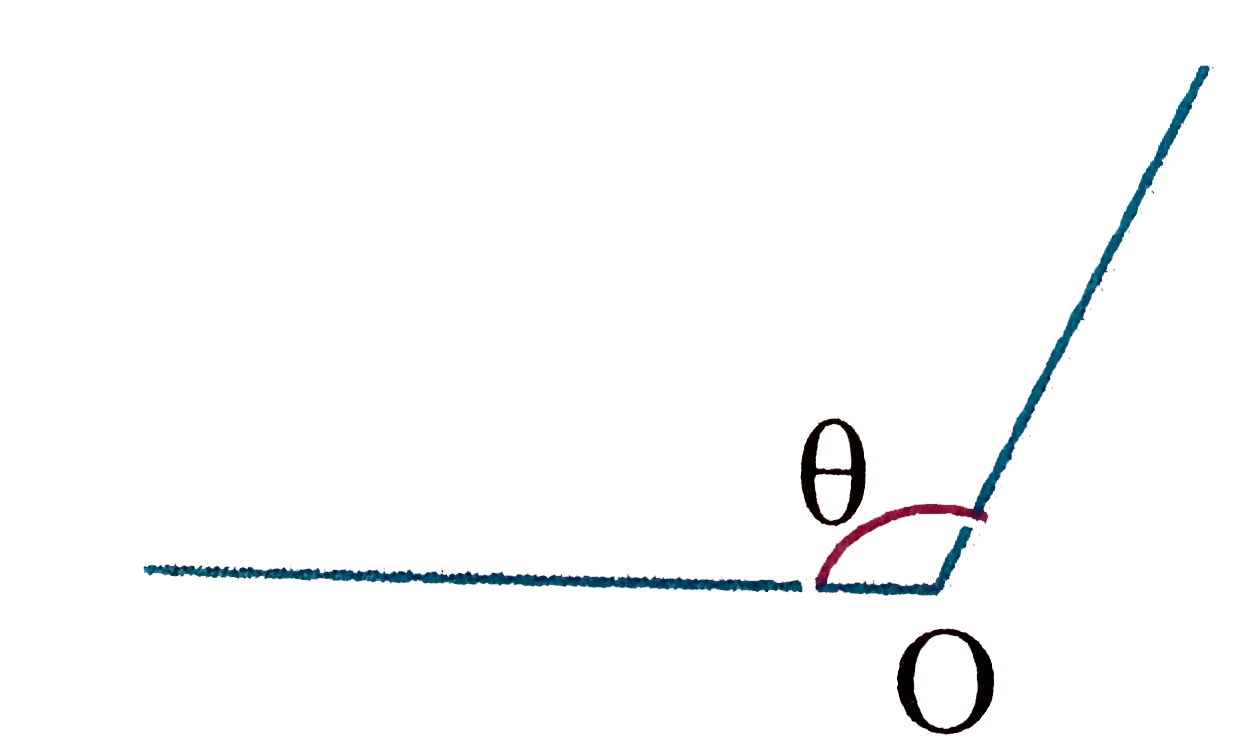 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2) - Question 2 - Select One
A smooth rod length l is kept inside a trolley at an angle θ as shown in the figure. What should be the acceleration a of the trolley so that the rod remain in equilibrium with respect to it?
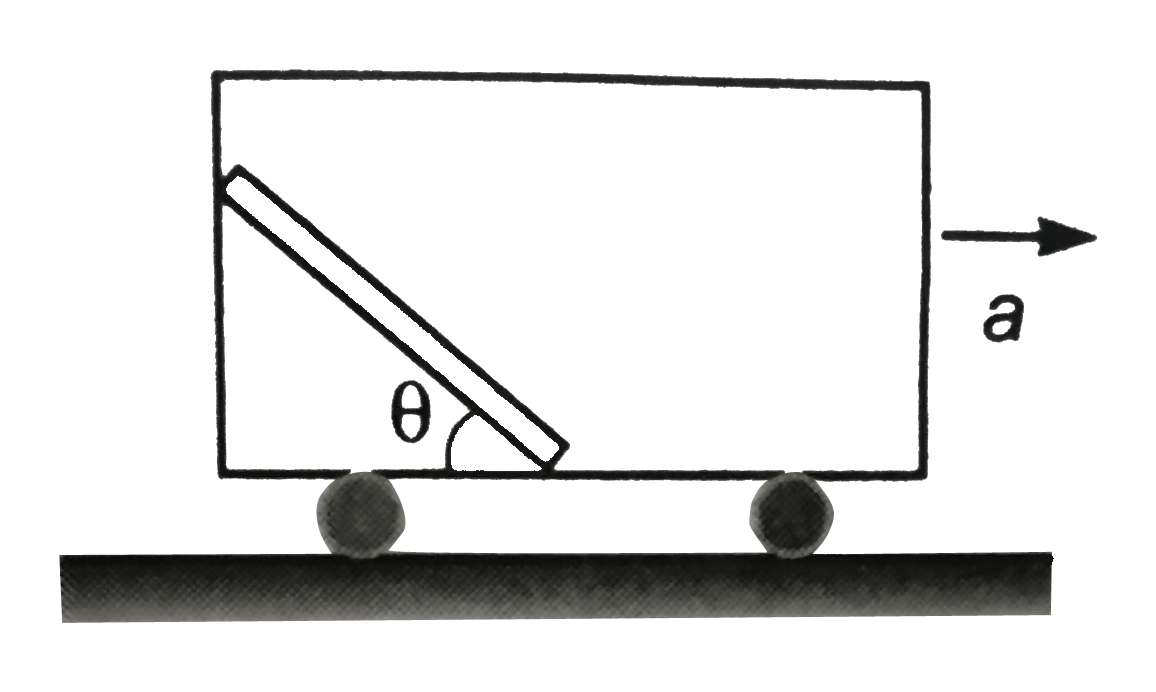 AgtanθBgcosθCgsinθDgcotθ
AgtanθBgcosθCgsinθDgcotθ - Question 3 - Select One
A uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.A60∘B30∘C45∘D37∘
A smooth rod length l is kept inside a trolley at an angle θ as shown in the figure. What should be the acceleration a of the trolley so that the rod remain in equilibrium with respect to it?
 View Solution
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the angle 0 if the density of the material of the rod is half of the density of water.View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.
 View Solution
View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.
 View Solution
View SolutionA uniform rod of length L pivoted at the bottom of a pond of depth L/2 stays in stable equilibrium as shown in the figure.

Find the force acting at the pivoted end of the rod in terms of mass m of the rod.View Solution


 .
.