A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is

1.5R
√3R
3R
2√3R
The correct Answer is:B
yCM=m1y1+m2y2m1+m2
=ρx13πR2h×h4=ρ×23πR3×3R8ρ×13πR2h+ρ×23πR3

⇒h=√3R
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE20videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE34videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
Similar Questions
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown in the figure. The centre of mass of the.composite solid lies at the centre of base of the cone. The height of the cone is √xR. Find x.
'(##CEN_KSR_PHY_JEE_C08_E01_017_Q10##)'View SolutionFind the centre of mass of a uniform solid cone.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, so as to have a common face. The centre of mass of the composite solid lies on the common face. The height of the cone is:
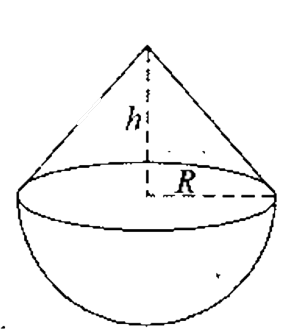 A1.5RB√3RC3RD2√3R
A1.5RB√3RC3RD2√3R - Question 2 - Select One
The centre of mass of a solid cone along the line form the center of the base to the vertex is at
AOne-fourth of the heightBOne-third of the heightCOne-fifth of the heightDNone of these - Question 3 - Select One
A solid hemisphere and a solid cone have a common base and are made of same material. The centre of mass of the common structure coincides with the centre of the common base. If R is the radius of hemisphere and h is height of the cone, then
 AhR=√3BhR=1√3ChR=3DhR=13
AhR=√3BhR=1√3ChR=3DhR=13
A right circular cone of radius R and height 2R is placed on a hemisphere of radius R. Locate c.m. of the combined mass from O.
 View Solution
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
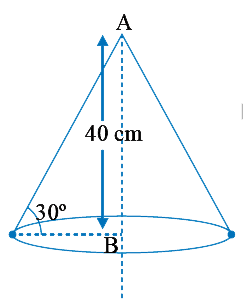 View Solution
View SolutionA uniform solid cone of height 40 cm is shown in figure. The distance of centre of mass of the cone from point B (centre of the base) is :
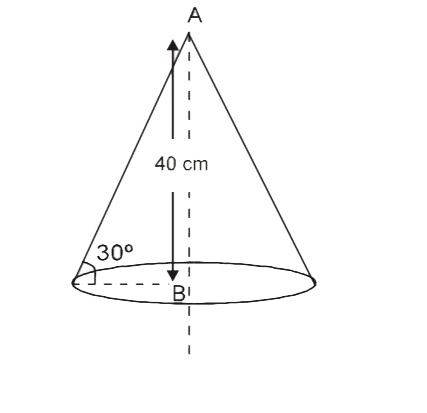 View Solution
View SolutionA solid right circular cylinder is attached to a hemisphere of equal base. If the C.G. of the combined solid is at the centre of the base, then the ratio of the radius and height of the cylinder is
View SolutionA solid metallic sphere of radius 6.3 cm is melted and recast into a right circular cone of height 25.2 cm. What is the ratio of the diameter of the base to the height of the cone ?
View Solution

