A uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω=(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
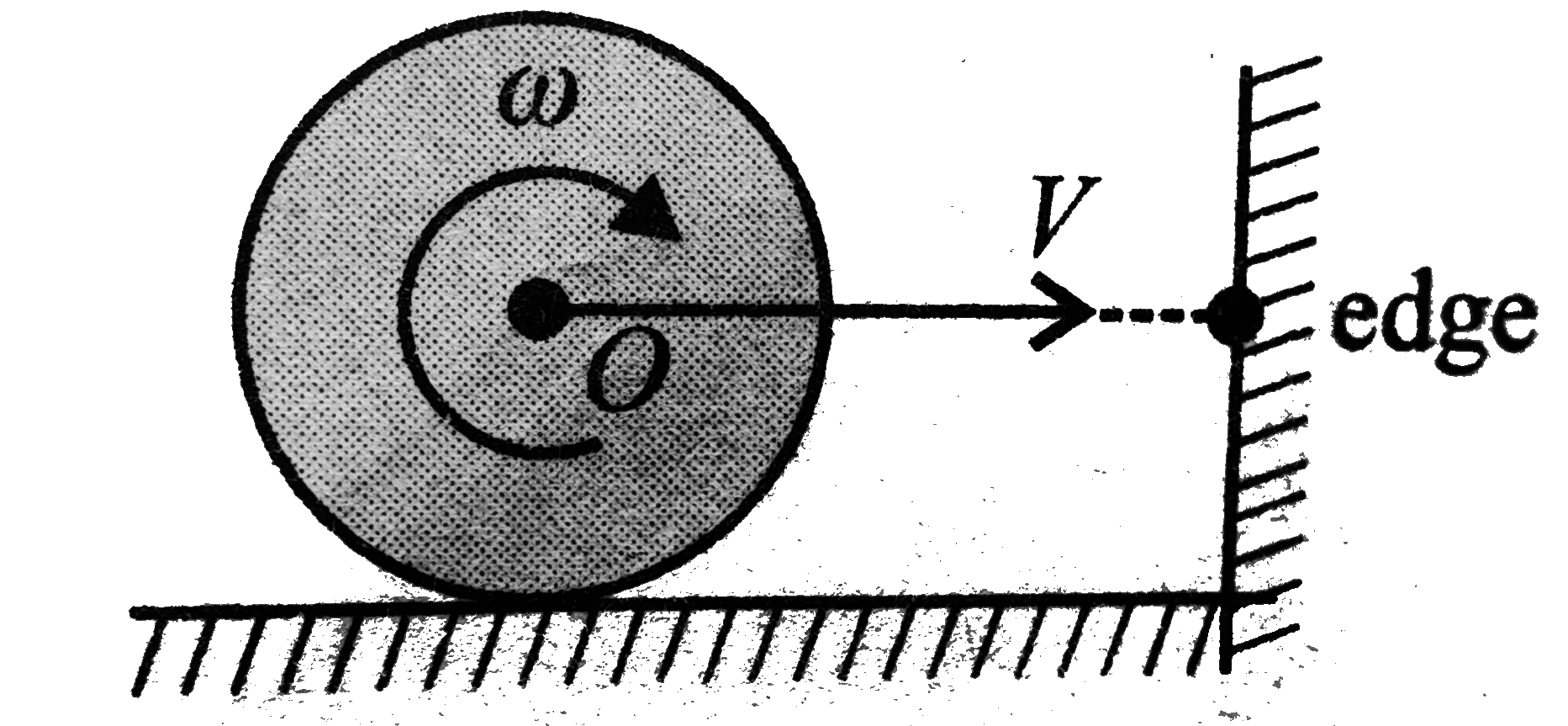
V
V5
3V5
V6
The correct Answer is:A
Impulse provided by the edge in the horizontal direction
∫Ndt=−mV'−(mV)..i
Friction impulse in the vertical direction
μR∫Ndt=25mr2(VR)…….ii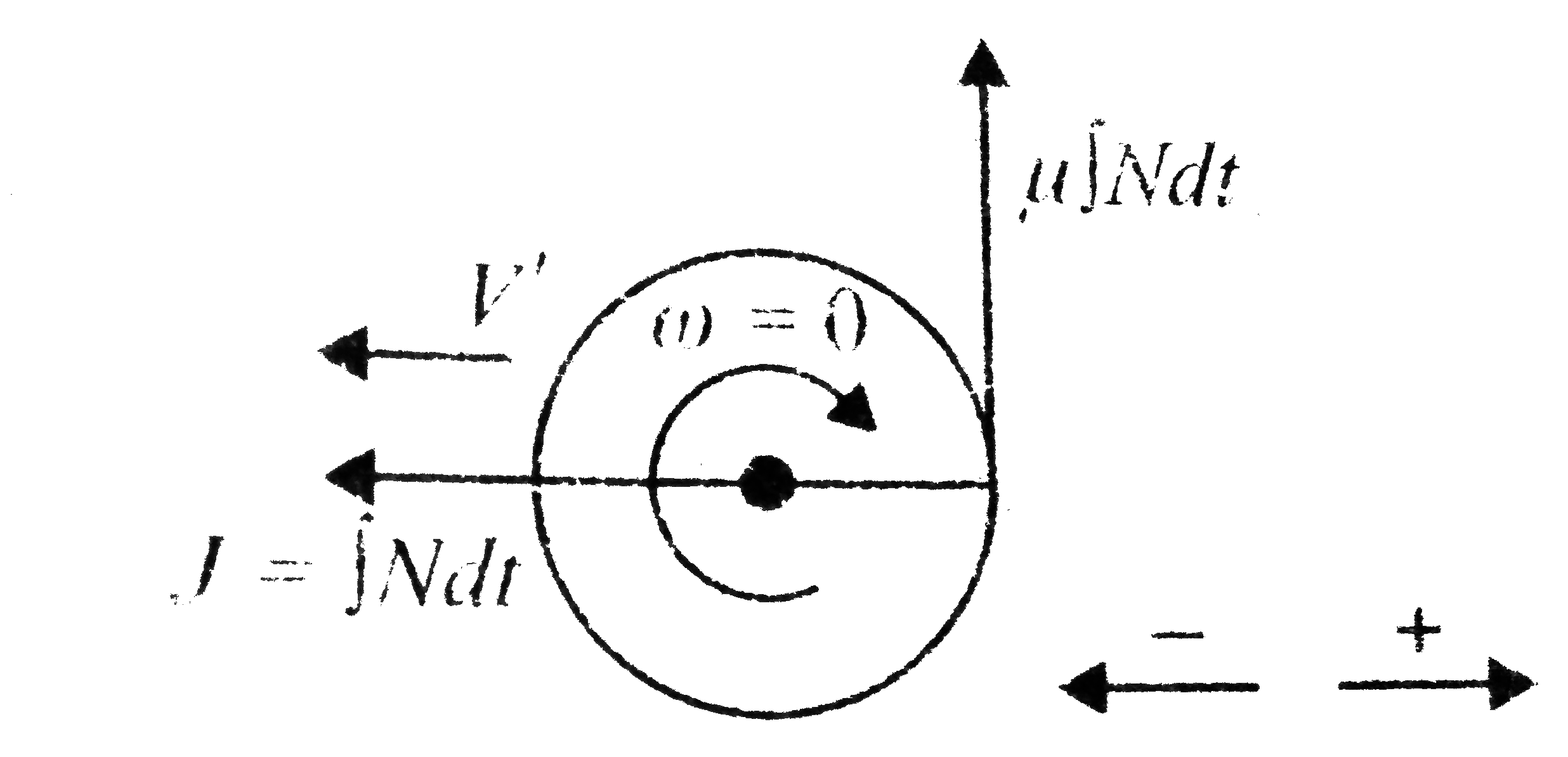 
Form eqn i annd ii we get
∫Ndt=2mV and V'=V
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A sphere of mass m moving with velocity v collides head-on with another sphere of the same mass at rest. If the coefficient of resistitution e=1/2, then what is the ratio of final velocity of the second sphere to the intial velocity of the first sphere ?
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
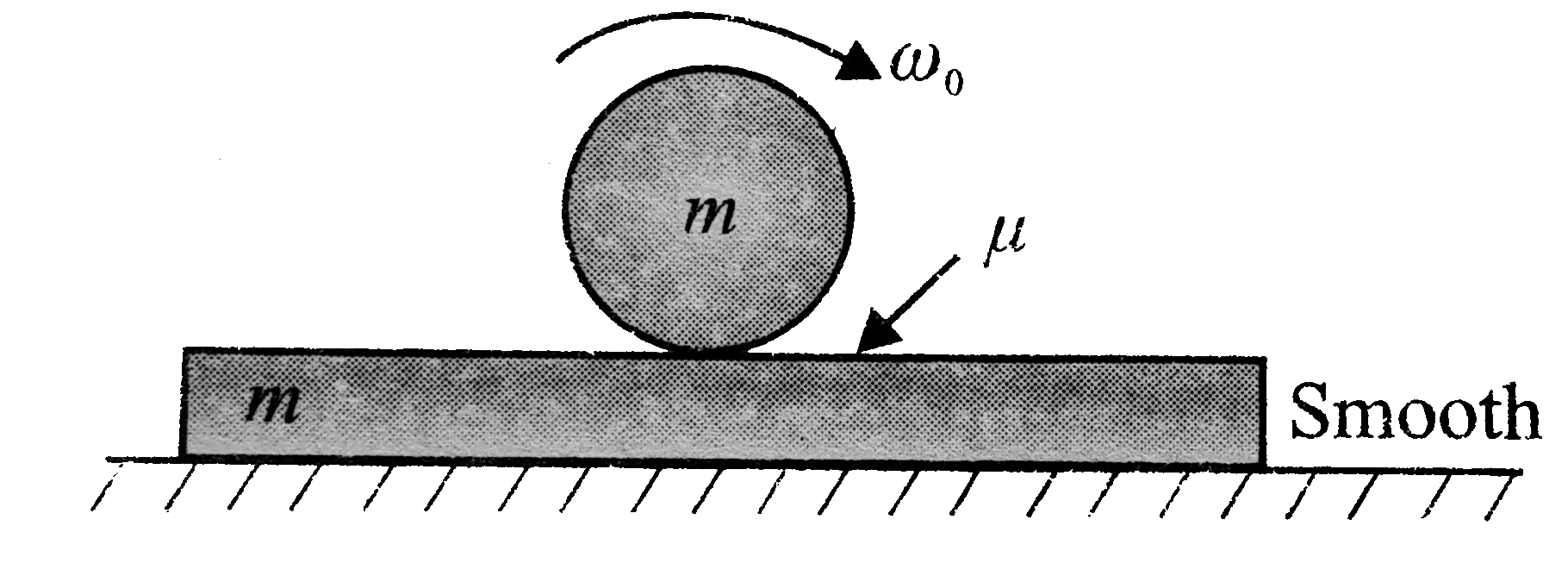
Find the velocity of the sphere after the pure rolling startsView Solution
Knowledge Check
- Question 1 - Select One
A uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity v and angular velocity ω=(v=ωr). The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to
AvBv5C3v5Dv6 - Question 2 - Select One
A sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
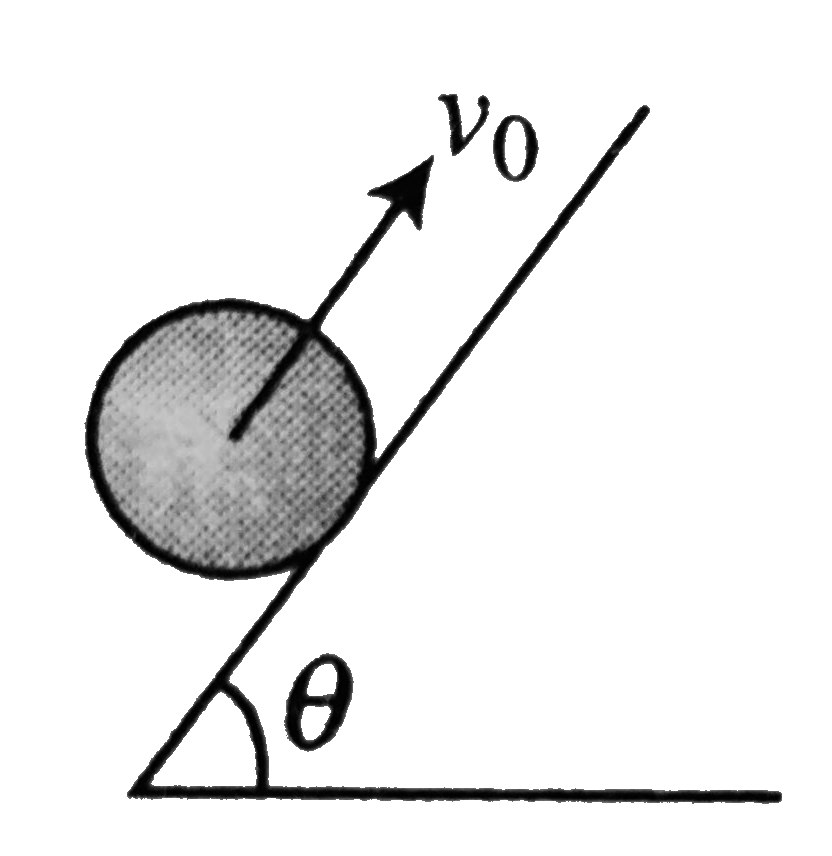Av0gcosθBv0gsinθCv0sinθgDnone - Question 3 - Select One
A sphere is performing pure rolling on a rough horizontal surface with constant angular velocity. Frictional force acting on the sphere is zero.
Velocity of contact point is zero.AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.
A solid sphere of radius 'r' is rolling with velocity V on a smooth plane. The total kinetic energy of sphere is
View SolutionA sphere is moving on a smooth surface with linear speed v0 and angular velocity ω0. It finds a rough inclined surface and it starts climbing up:
View SolutionA smooth sphere is moving on a horizontal surface with velocity vector 2ˆi+2ˆj immediately before it hits a vertical wall. The wall is parallel to ˆj vector and the coefficient of restitution between the sphere and the wall is e=1/2. The velocity vector of the sphere after it hits the wall is
View SolutionA solid sphere is set into motion on a rough horizontal surface with a linear velocity v in the forward direction and an angular velocity v/R in the anticlockwise direction as shown in the figure. Find the linear speed of the sphere, when it stops rotating.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
Find the velocity of the sphere after the pure rolling startsView Solution