A uniform thin circular ring of mass m(m=0.4kg) and radius R has a small particle of the same mass m fixed on it as shown in Fig. The line joining the particle to centre is initially horizontal. The ground is frictionless. Find the contact force (magnitude) exerted by the ground on the ring, when the system is released from rest.

The correct Answer is:32mg
Applying torque equation about centre of mas
τCM=ICMα………i
⇒NR2=(ICM)α…ii
ICM=mR2+m(R2)2+m(R2)2=32mR2
The CM of system (ring+particle) will be at a distance R/2 from the centre of the ring.

2mg−N=2m(aCM)y .....iii
using constraint acceleration of centre of circle is zero
(ac)y=0
⇒R2α=(aCM_(y)).......iv
Form ii, iii and iv we get
N=32mg
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
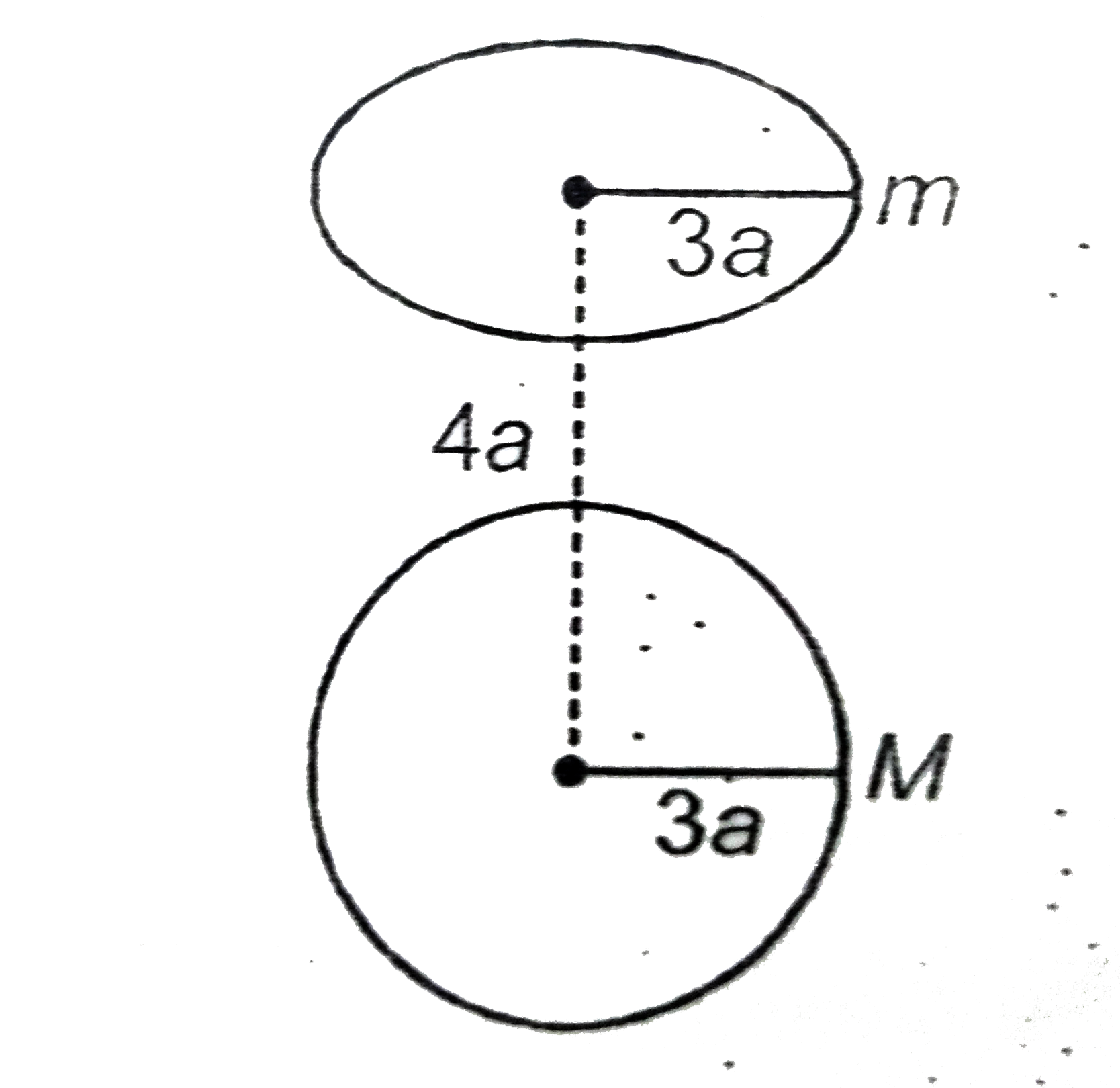 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
AGMm8r2BGMm4r2C√3GMm8r2DGMm8r3√3
A circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
View SolutionA ring mass m and radius R has three particle attached to the ring as shown in the figure. The centre of the centre v0. Find the kinetic energy of the system. (Slipping is absent).
 .View Solution
.View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View Solution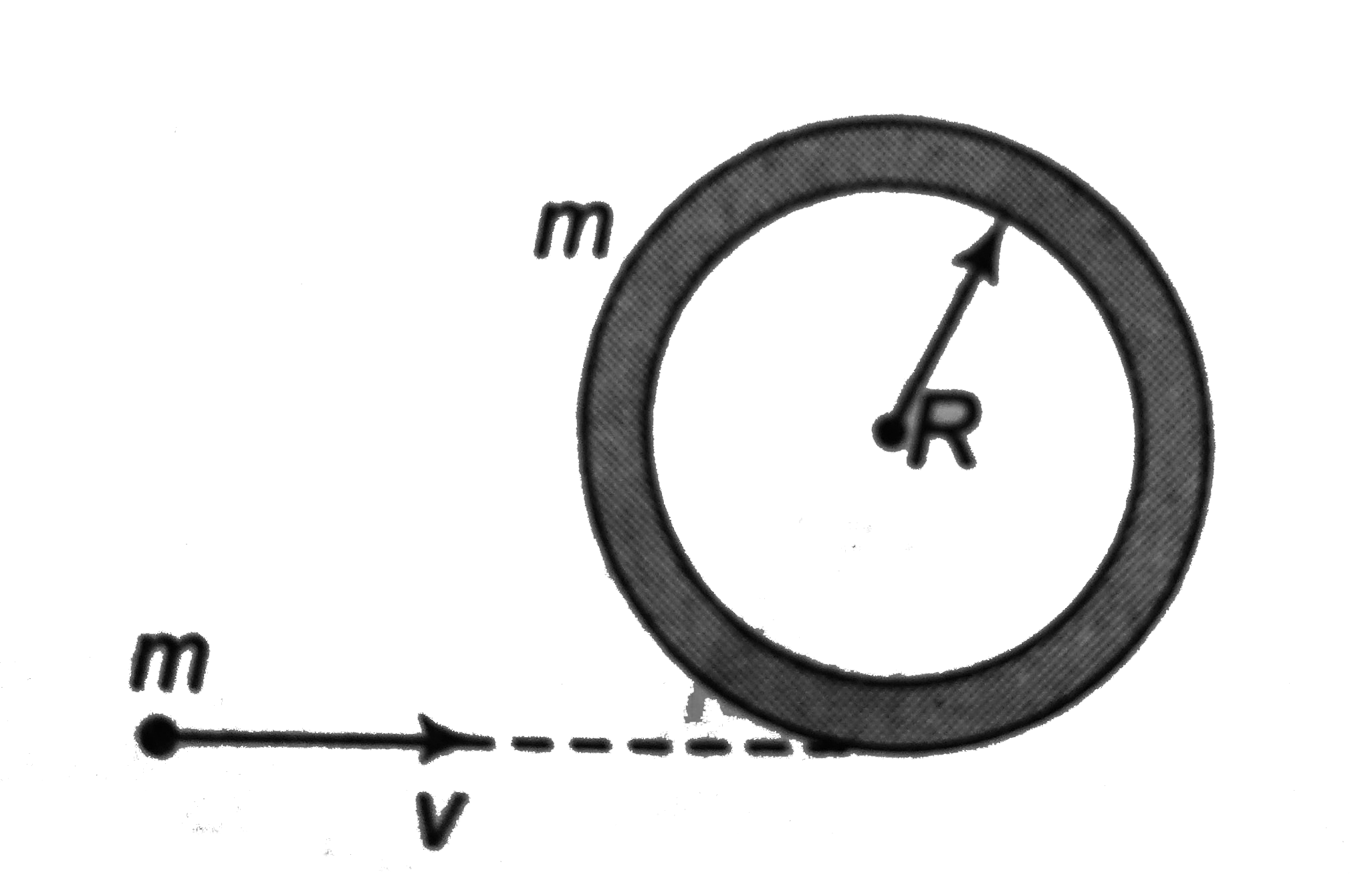
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring isView SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2rView SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

x>2RView Solution
