A weight W is suspended by using two strings. One of the strings makes an angle of with the vertical. What should be the direction of the other string so that the tension in it becomes minimum? Find the tension in each string at this position.
Let the angle between the two strings be Fig.
Given that the angle between the weight W and the first string
=
Hence, angle between the weight and the second string
=
For equilibrium using Lami.s theorem,
For to be minimum, sin should be maximum i.e., sin =1 or . Hence the tension in the second string will be minimum when it is at right angles to the first string.
At this setting,
Also ,
or,
.

Topper's Solved these Questions
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
18 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - EXERCISE (Multiple Choice Questions )
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner
14 Videos
Similar Questions
Knowledge Check
Tension in the string is minimum when the pendulum is at
Amean positionBextreme positionCmid way between mean and extreme positionDany positionIf a bodyy is tied to a string and whirled in vertical circle, then the tension in the string at the highest position is
AmaximumBminimumCbetween maximum and minimum valuesDzeroIf in the previous problem, the breaking strength of the string is 2mg, then the minimum tension in the string will be
AmgBmg4C3mg4Dmg2
A block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionA weight W is supported by two strings inclined at 60∘ and 30∘ to the vertical. The tensions in the strings are T1 and T2 as shown. If these tensions in the strings are to be determined in terms of W using a triangle of force, which of these triangles should you draw? (block is in equilibrium)
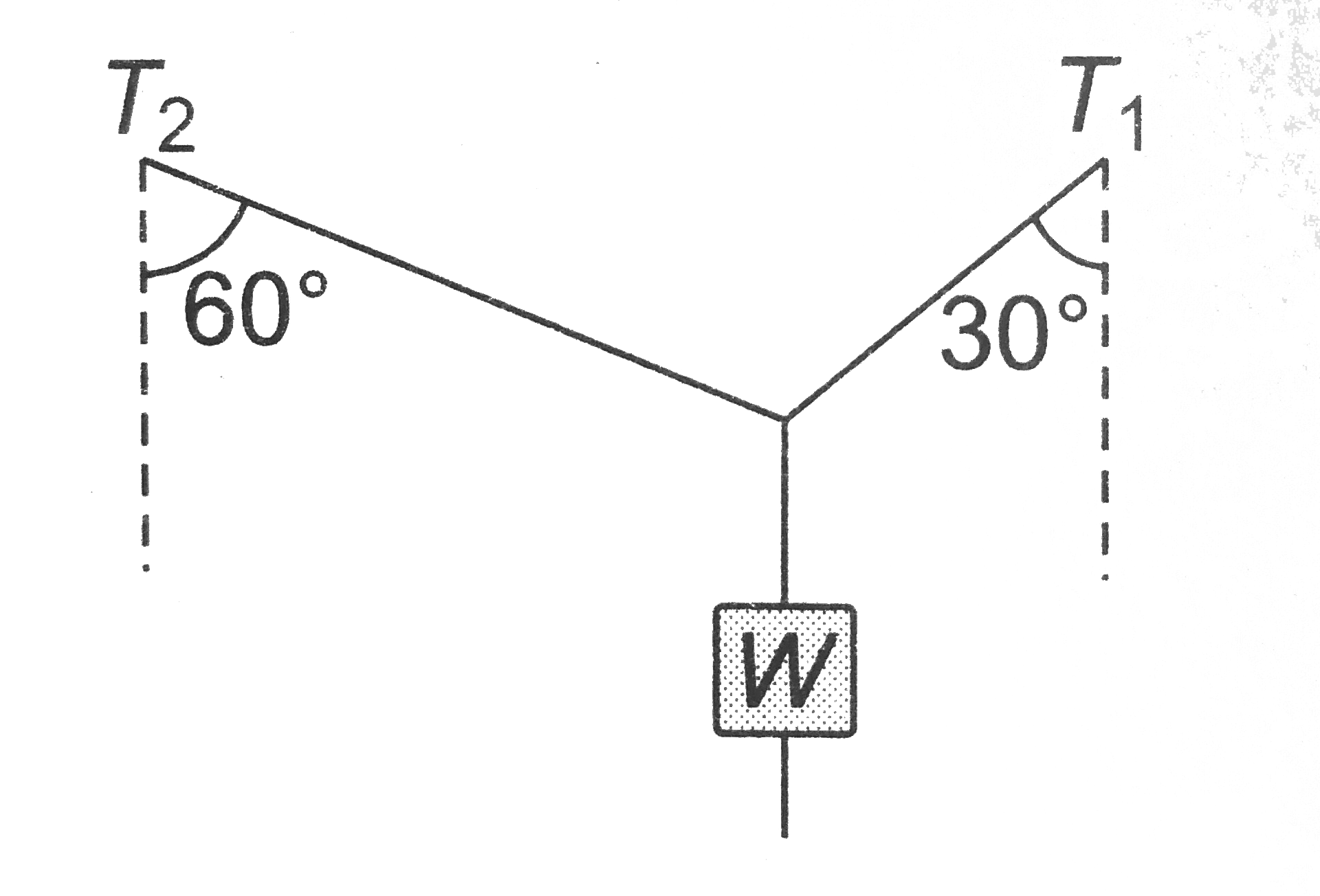
View SolutionA body of weight 200N is suspended with the help of strings as show in Find the tensions in the strings
 .
.
View SolutionA body of mass √3 kg is suspended by a string to rigid support.The body is pulled horizontally by a force F until the string makes an angle of 30∘ with the vertical.The value of F and tension in the string are
View SolutionA small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle 'a' with the vertical in equilibrium. Then the tension in the string is :
View Solution
