A wheel ios rolling without sliding on a horizontal surface. The centre of the wheelk moves with a constant speed v0. Consider a point P on the rim which is at the top at time t=0. The square of speed of point P is plooted against time t. The correct plot is (R is radius of the wheel)
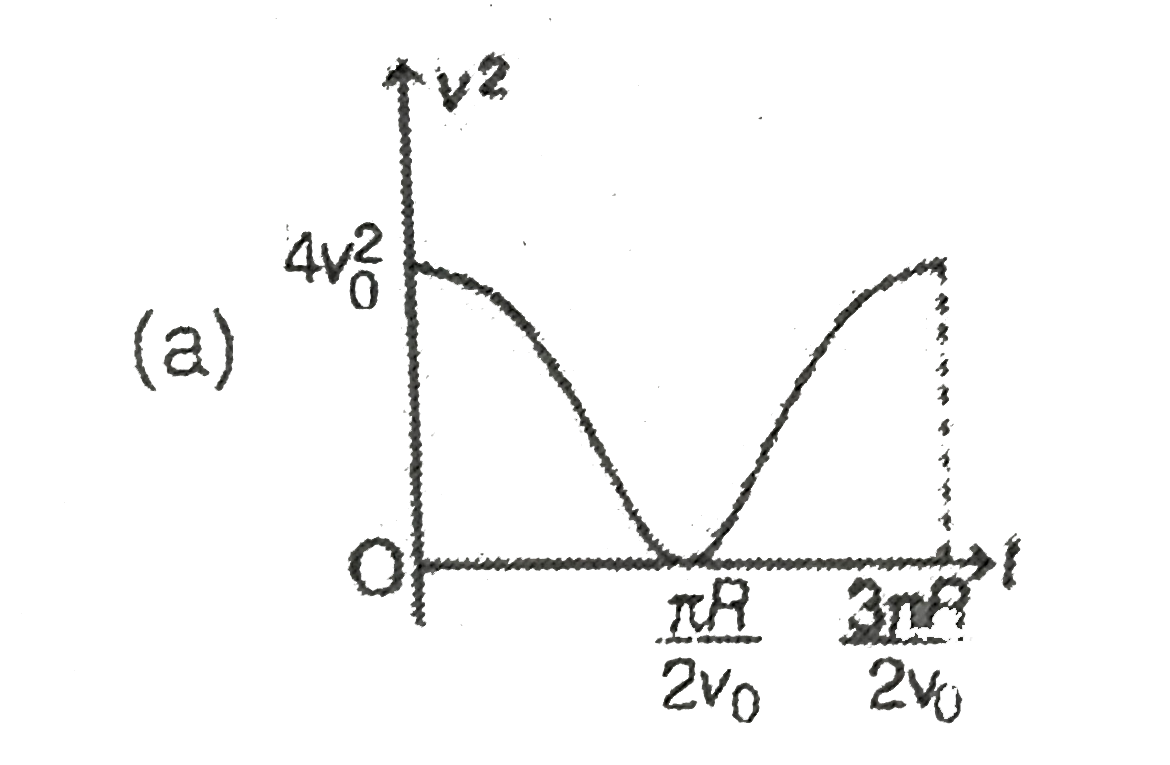

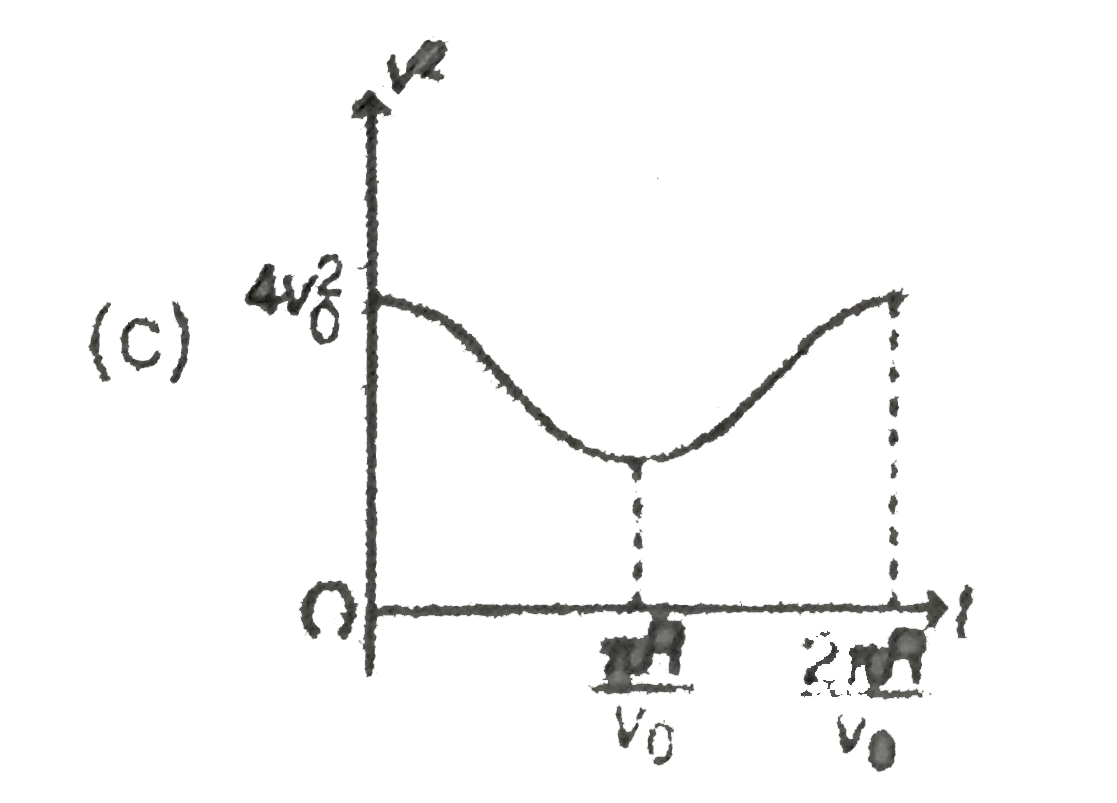
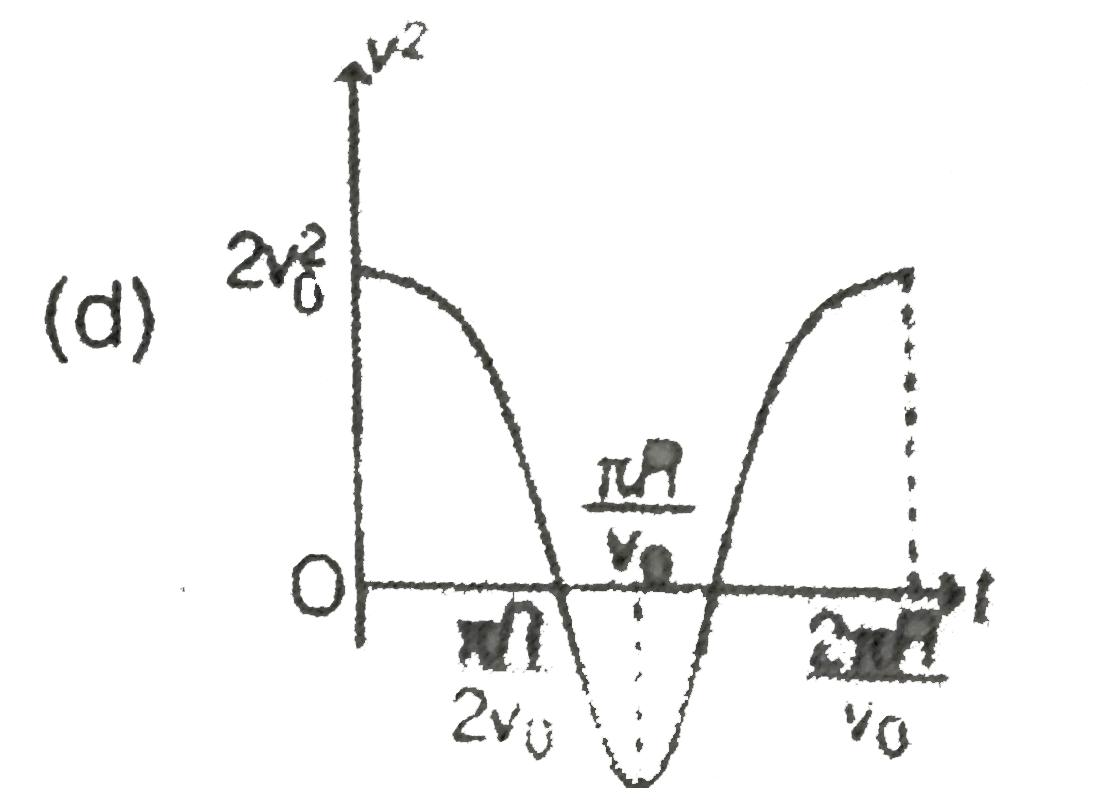
The correct Answer is:B
To solve the problem of a wheel rolling without sliding on a horizontal surface, we need to analyze the motion of a point on the rim of the wheel. Here's a step-by-step breakdown of the solution:
Step 1: Understand the motion of the wheel
The wheel rolls without slipping, which means that the point of contact with the ground is momentarily at rest. The center of the wheel moves with a constant speed v0.
Step 2: Identify the position of point P
At time t=0, point P is at the top of the wheel. As the wheel rolls, point P will move in a circular path around the center of the wheel.
Step 3: Determine the speed of point P
The speed of point P can be expressed as the sum of the translational speed of the center of the wheel and the rotational speed due to the wheel's rotation.
- The translational speed of the center is v0.
- The rotational speed at the top of the wheel is vrot=Rω, where R is the radius of the wheel and ω is the angular velocity.
Since the wheel rolls without slipping, we have the relationship:
v0=Rω
Thus, the speed of point P at any time t can be expressed as:
vP(t)=v0+Rω(t)
Step 4: Express angular velocity in terms of time
The angular position θ of the wheel as a function of time can be expressed as:
θ(t)=ωt
The angular velocity ω is constant, so:
ω=v0R
Step 5: Calculate the speed of point P
At time t, the speed of point P becomes:
vP(t)=v0+R(v0Rsin(ωt))
This simplifies to:
vP(t)=v0(1+sin(ωt))
Step 6: Find the square of the speed
To plot the square of the speed against time:
v2P(t)=(v0(1+sin(ωt)))2
Expanding this gives:
v2P(t)=v20(1+2sin(ωt)+sin2(ωt))
Step 7: Analyze the behavior of v2P(t)
The term sin2(ωt) oscillates between 0 and 1, and thus the square of the speed will oscillate between:
v20(1+0) and v20(1+2+1)=4v20
This indicates that v2P(t) will have a periodic behavior with a maximum and minimum value.
Step 8: Identify the correct plot
Given that the square of the speed oscillates sinusoidally, the correct plot will show a periodic function that varies between v20 and 4v20.
Conclusion
The correct plot of the square of the speed of point P against time t is a sinusoidal curve oscillating between v20 and 4v20.
---
The wheel rolls without slipping, which means that the point of contact with the ground is momentarily at rest. The center of the wheel moves with a constant speed v0.
At time t=0, point P is at the top of the wheel. As the wheel rolls, point P will move in a circular path around the center of the wheel.
The speed of point P can be expressed as the sum of the translational speed of the center of the wheel and the rotational speed due to the wheel's rotation.
- The rotational speed at the top of the wheel is vrot=Rω, where R is the radius of the wheel and ω is the angular velocity.
v0=Rω
Thus, the speed of point P at any time t can be expressed as:
vP(t)=v0+Rω(t)
The angular position θ of the wheel as a function of time can be expressed as:
θ(t)=ωt
The angular velocity ω is constant, so:
ω=v0R
At time t, the speed of point P becomes:
vP(t)=v0+R(v0Rsin(ωt))
This simplifies to:
vP(t)=v0(1+sin(ωt))
To plot the square of the speed against time:
v2P(t)=(v0(1+sin(ωt)))2
Expanding this gives:
v2P(t)=v20(1+2sin(ωt)+sin2(ωt))
The term sin2(ωt) oscillates between 0 and 1, and thus the square of the speed will oscillate between:
v20(1+0) and v20(1+2+1)=4v20
This indicates that v2P(t) will have a periodic behavior with a maximum and minimum value.
Given that the square of the speed oscillates sinusoidally, the correct plot will show a periodic function that varies between v20 and 4v20.
The correct plot of the square of the speed of point P against time t is a sinusoidal curve oscillating between v20 and 4v20.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is

View SolutionA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.

View SolutionA ring rolls without slipping on the ground. Its centre C moves with a constant speed u.P is any point on the ring. The speed of P with respect to the ground is v.
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If mass of the sphere is m and its radius be R, then the angular momentum of the sphere about the point of contact is.
View SolutionA circular disc of radius R rolls without slipping along the horizontal surface with constant velocity v0 . We consider a point A on the surface of the disc. Then, the acceleration of point A is
View SolutionA sphere of mass M rolls without slipping on rough surface with centre of mass has constant speed v0. If its radius is R, then the angular momentum of the sphere about the point of contact is.
View SolutionThe centre of a wheel rolling without slipping on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the centre of wheel will be moving with speed
View SolutionThe center of a wheel rolling on a plane surface moves with a speed v0. A particle on the rim of the wheel at the same level as the center will be moving at speed
View SolutionConsider a wheel rolls without slipping and its centre moves with constant acceleration a. Find the acceleration of points O,P,Q and S when linear velocity of the centre of wheel is v.
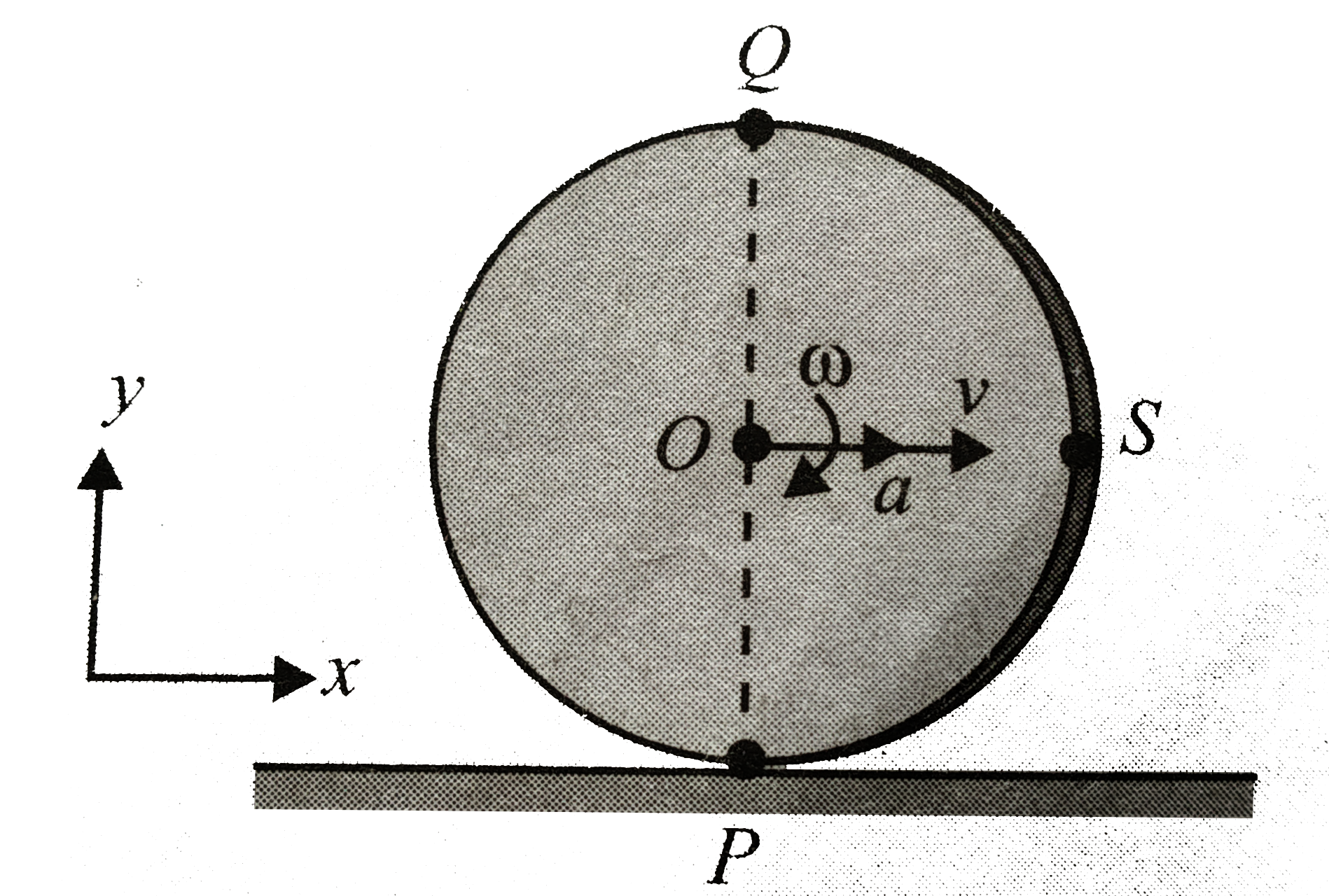
View SolutionA conducting rim of radius R rolls without slipping on a horizontal surface . The speed of the ring 's centre of mass is v0 . A uniform magnetic field B perpendicular to the ring 's plane is swithched on. The emf induced across point of contact and the topmost point of the rim is 2Bv0R.

View Solution
