A wide copper strip of width l is bent into piece of slendder tubing of radius R with two plane extension as shown (Fig. 1.12). A current I flows through the strip, distributed uniformly over its width. Ib this way, one-turn solenoid has been formed (a) Derive an expression for the magnetic field in the tubular part.
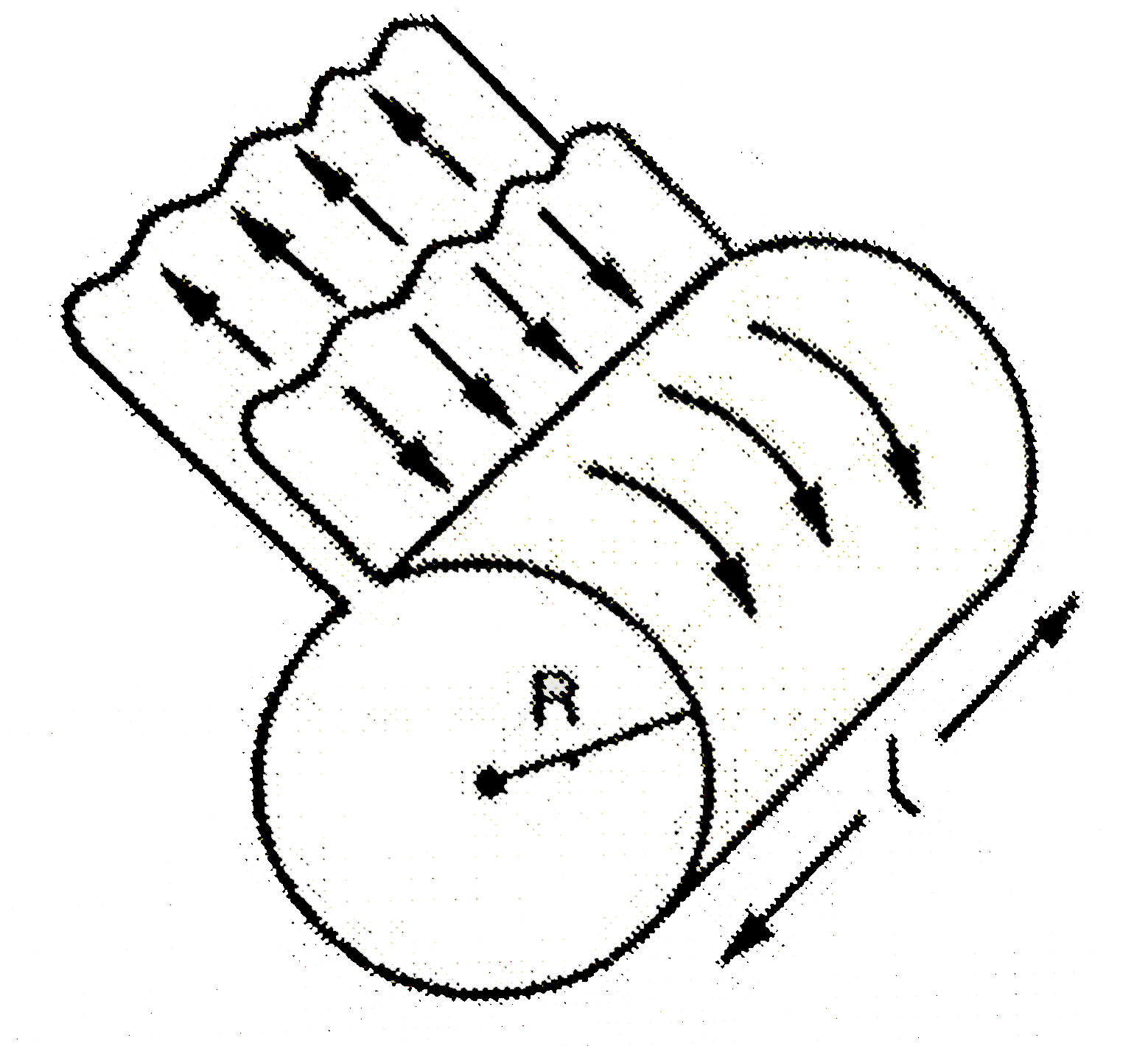
The correct Answer is:μ0il
Topper's Solved these Questions
Similar Questions
A thin conducting strip of width his tightly wound in the shape of a very long cylindrical coil with cross-sectional radius R to make a single layer straight solenoid as shown in figure-4.81. A direct current I flows through the strip. Find the magnetic induction inside and outside the solenoid as a function of the distance r from its axis.
 View Solution
View SolutionA long cylindrical conductor of radius R has two cylindrical cavities of diameter R through its entire length, as shown in the figure. There is a current I through the conductor distributed uniformly in its entire cross section (apart from the cavity region). Find magnetic field at point P at a distance r=2R from the axis of the conductor (see figure).
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wider conductor strip of width x is bent into a slender tubing of radius r with its two ends forming two plane extensions. A current I flowing through it gives magnetic field in tubular portion given by
Aμ0I2πrBμ0I2xCμ0IπxDμ0Ix - Question 2 - Select One
A certain transmission line (very long) is constructed from two thin metal plates (parallel to each other) of width b, which are separated by a very small distance ‘h’ lt lt ‘b’ . The current travels down one strip and back along the other, and it is distributed uniformly over the surface of the plates as shown in figure. Neglect fringing field at ends of plates.
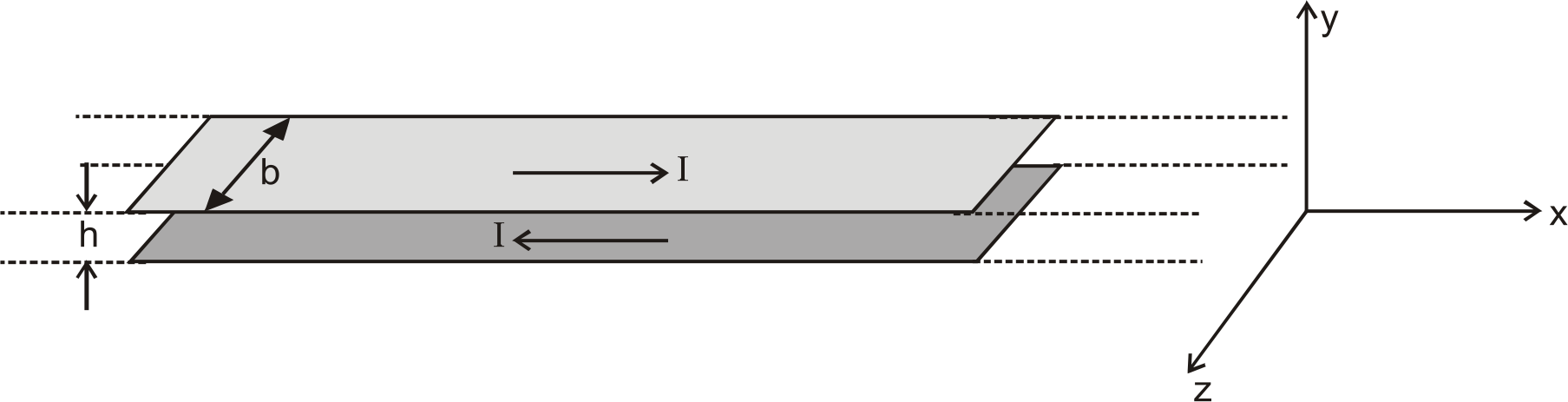
Magnetic field between the space of two plates isAμ0l2h(ˆk)Bμ0lb2h2(ˆk)Cμ0lb(−ˆk)Dμ0lhb2(−ˆk) - Question 3 - Select One or More
Current flows through a straight cylindrical conductor of radius r. The current is distributed uniformly over its cross-section. The magnetic field at a distanace x from the axis of the conductor has magnitude B:
AB=0 at the axisBB∝x for 0≤x≤rCB∝1/x for x>rDB is maximum for x=r
A thin conducting strip of width h=2.0cm is tightly woudnd in the spahe of a very long coil with cross-seciton radius R=2.5cm to make a single-layer straight solenoid. A direct curretnt I=5.0 A flows through the strip. Find the magnetic inductin inside and outside the solenoid as a funcition of the distanance r from its axis.
View SolutionA long cylindrical conductor of radius a has two cylindrical cavities of diameter a through its entire length as shown in cross-section in figure. A current I is directed out of the page and is uniform throughout the cross-section of the conductor. Find the magnitude and direction of the magnetic field in terms of μ0,I,r and a.
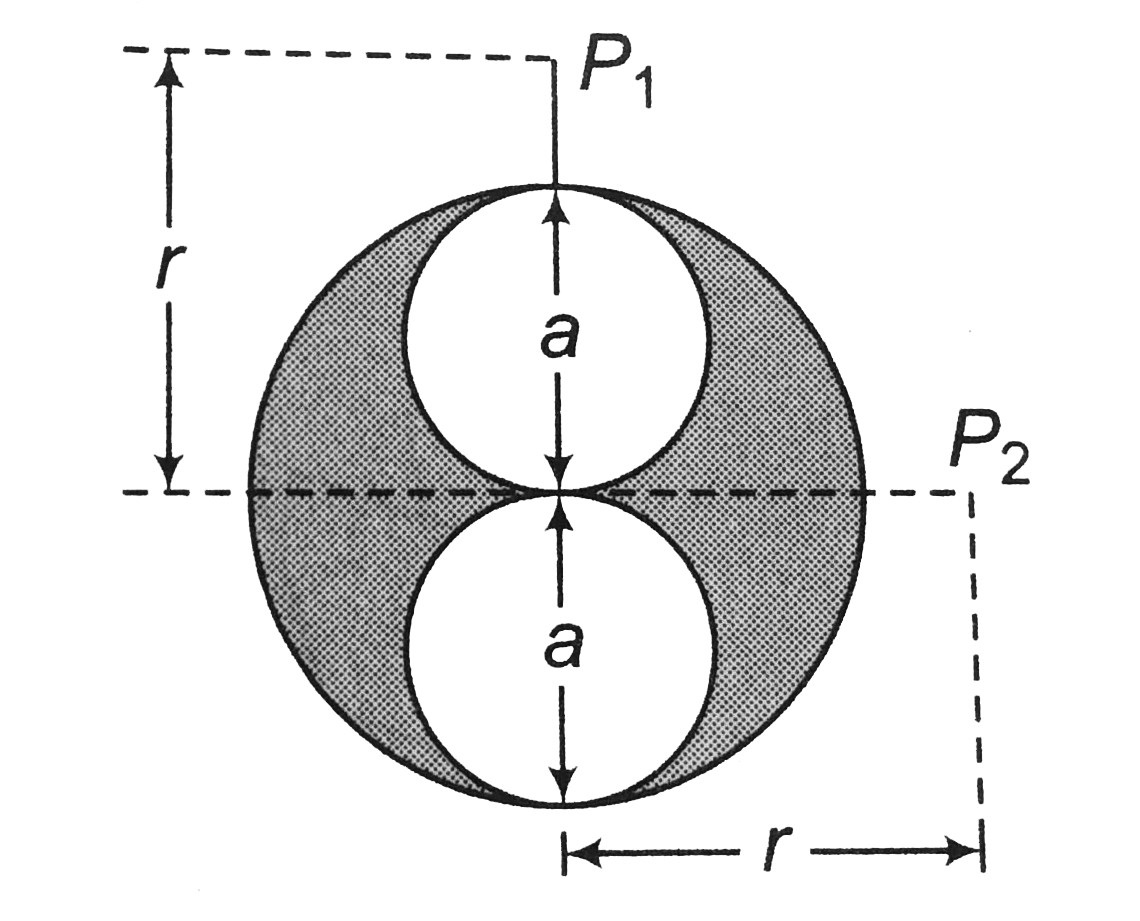
(a) at point P1 and (b) at point P2View SolutionA wire of length L is bent around in the form of a coil having N turns of same radius . If a steady current I flows through it in a clockwise direction, find the magnitude and direction of the magnetic field produced at its centre.
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
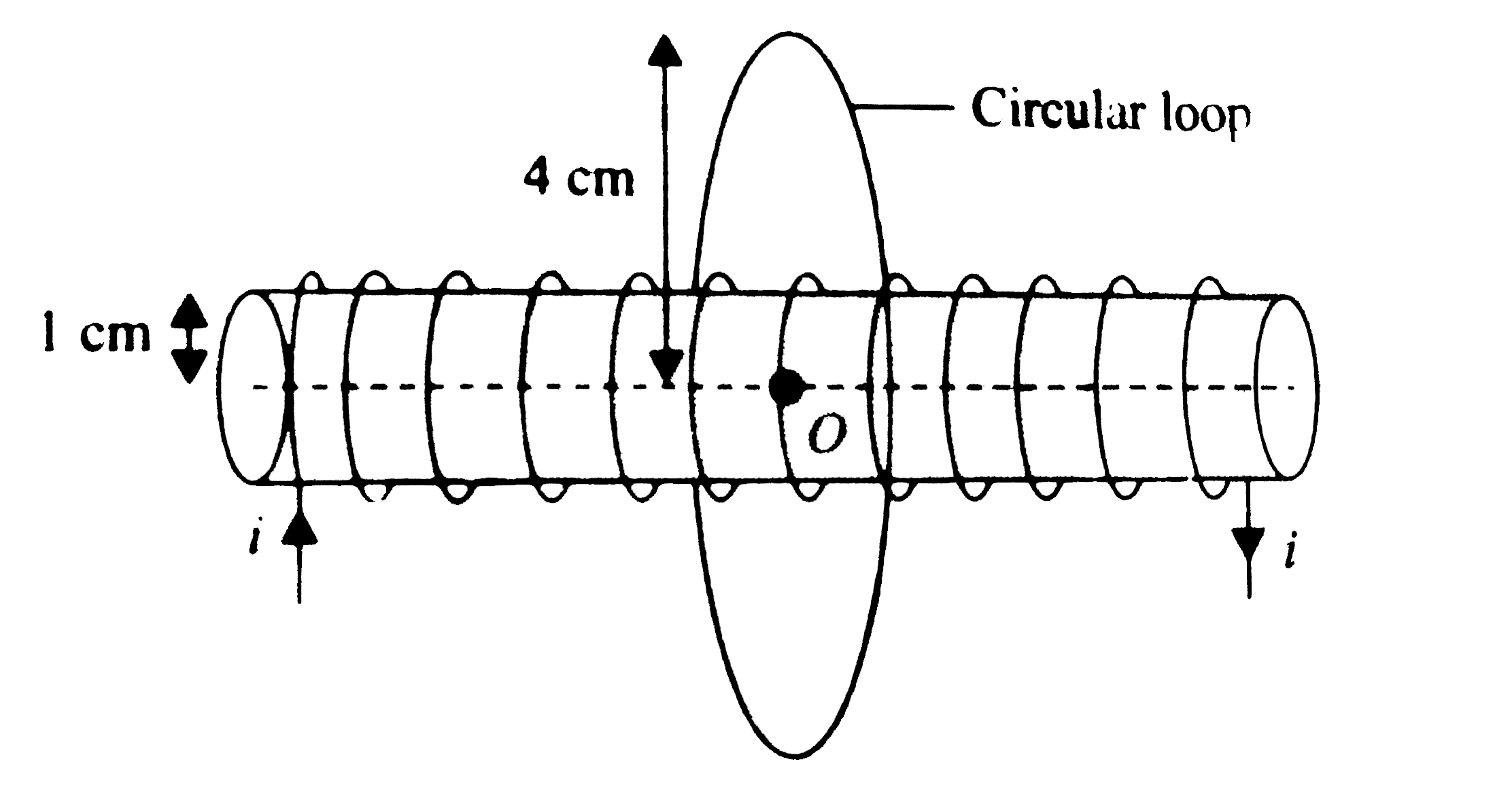
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoidView SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoidView Solution

