(a)Compare the otto cycle with diesel cycle.
(b)Explain the working of a diesel engine. Derive an expression for its efficiency.
Step-by-Step Solution
1. Heat Addition Process:
- Otto Cycle: Heat is added at a constant volume.
- Diesel Cycle: Heat is added at a constant pressure.
2. Compression Ratio:
- Otto Cycle: The compression ratio is lower, typically ranging from 6 to 10.
- Diesel Cycle: The compression ratio is higher, ranging from 14 to 22.
3. Efficiency:
- Otto Cycle: Generally has higher efficiency compared to the Diesel cycle.
- Diesel Cycle: Has lower efficiency compared to the Otto cycle.
4. Fuel-Air Mixture:
- Otto Cycle: An air-fuel mixture is introduced at the inlet valve.
- Diesel Cycle: Only air is supplied at the inlet valve.
5. Fuel Injection Timing:
- Otto Cycle: Fuel is injected during the suction stroke.
- Diesel Cycle: Fuel is injected at the end of the compression stroke.
Part (b): Explain the Working of a Diesel Engine and Derive an Expression for its Efficiency
1. Overview of Diesel Engine Operation:
- The diesel engine operates on the Diesel cycle, which consists of four stages: two adiabatic (isentropic) processes and two isobaric (constant pressure) processes.
2. Stages of the Diesel Cycle:
- Stage 1 to Stage 2: The air is compressed adiabatically, raising its temperature and pressure.
- Stage 2 to Stage 3: Heat is added at constant pressure (Q_in). The heat added can be expressed as:
Qin=Cp(T3−T2)
- Stage 3 to Stage 4: The gas expands adiabatically, doing work on the piston.
- Stage 4 to Stage 1: Heat is rejected at constant volume (Q_out). The heat rejected can be expressed as:
Qout=Cv(T4−T1)
3. Work Done:
- The work done (W) by the engine can be calculated as the difference between the heat supplied and the heat rejected:
W=Qin−Qout=Cp(T3−T2)−Cv(T4−T1)
4. Efficiency of the Diesel Engine:
- The efficiency (η) of the diesel engine is defined as the ratio of the work done to the heat supplied:
η=WQin=Cp(T3−T2)−Cv(T4−T1)Cp(T3−T2)
- Rearranging this gives:
η=1−Cv(T4−T1)Cp(T3−T2)
- Using the relation CpCv=γ, we can express the efficiency as:
η=1−T4−T1γ(T3−T2)
- Otto Cycle: Heat is added at a constant volume.
- Diesel Cycle: Heat is added at a constant pressure.
- Otto Cycle: The compression ratio is lower, typically ranging from 6 to 10.
- Diesel Cycle: The compression ratio is higher, ranging from 14 to 22.
- Otto Cycle: Generally has higher efficiency compared to the Diesel cycle.
- Diesel Cycle: Has lower efficiency compared to the Otto cycle.
- Otto Cycle: An air-fuel mixture is introduced at the inlet valve.
- Diesel Cycle: Only air is supplied at the inlet valve.
- Otto Cycle: Fuel is injected during the suction stroke.
- Diesel Cycle: Fuel is injected at the end of the compression stroke.
- The diesel engine operates on the Diesel cycle, which consists of four stages: two adiabatic (isentropic) processes and two isobaric (constant pressure) processes.
- Stage 1 to Stage 2: The air is compressed adiabatically, raising its temperature and pressure.
- Stage 2 to Stage 3: Heat is added at constant pressure (Q_in). The heat added can be expressed as:
Qin=Cp(T3−T2)
- Stage 3 to Stage 4: The gas expands adiabatically, doing work on the piston.
- Stage 4 to Stage 1: Heat is rejected at constant volume (Q_out). The heat rejected can be expressed as:
Qout=Cv(T4−T1)
- The work done (W) by the engine can be calculated as the difference between the heat supplied and the heat rejected:
W=Qin−Qout=Cp(T3−T2)−Cv(T4−T1)
- The efficiency (η) of the diesel engine is defined as the ratio of the work done to the heat supplied:
η=WQin=Cp(T3−T2)−Cv(T4−T1)Cp(T3−T2)
- Rearranging this gives:
η=1−Cv(T4−T1)Cp(T3−T2)
- Using the relation CpCv=γ, we can express the efficiency as:
η=1−T4−T1γ(T3−T2)
Topper's Solved these Questions
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SHORT ANSWER QUESTIONS30videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - VERY SHORT ANSWER QUESTIONS17videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS17videos
INTERNAL ENERGY
- BOOK - ICSECHAPTER - GRAVITATIONEXERCISE - FROM THE HUBBLE TELESCOP2videos
GRAVITATION
- BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)19videos
MOTION IN FLUIDS
Similar Questions
(a) What is a heat engine ?
Name the important part of a heat engine.
(b) Explain the working of a Carnot engine. Obtain an expression for its efficiency.View SolutionThe temperature-entropy diagram of a reversible engine cycle is given in the figure. Its efficiency is:
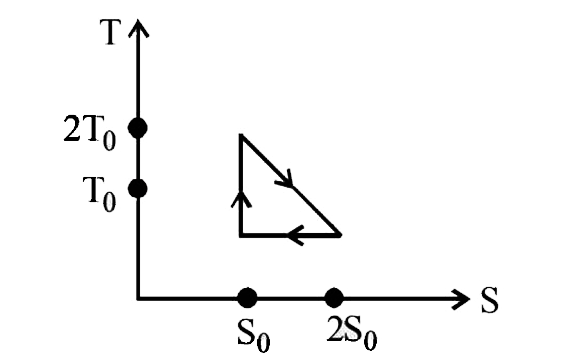 View Solution
View SolutionA carnot engine is operated between two reserviors at temperatures of 500 K and 400 K. The engine receives 840 Joules of heat from the source in each cycle. Calculate (a) the amount of heat rejected to sink in each cycle (b) the efficiency of the engine, and (c) the work done in each cycle.
View SolutionDraw a Carnot cycle and on the diagram mark the work done by the engine.
View SolutionThe temperature of food material in refrigerator is 4∘C and temperature of environment is 15∘C. If carnot cycle is used in its working gas, then find its carnot efficiency.
View Solution(a) Derive the expression for the torque acting on a current carrying placed in a magnetic field.
(b) Explain the significance of a radial magnetic when current carrying coil is kept in it.View SolutionA heat engine draws, 800 J of heat from its high temperature source and discards 600 J of exhaust heat into its cold-temperature reservoir each cycle. How much work does this engine perform per cycle, and what is its thermal efficiency?
View SolutionIf a Carnot engine works between 127∘Cand727∘C, then its efficiency is
View SolutionAssertion : The Carnot cycle is useful in understanding the performance of heat engines.
Reason : The Carnot cycle provides a way of deteriming the maximum possible efficiency achievable with reservoirs of given temperatures.View SolutionDescribe nitrogen cycle in nature. Explain its importance in plants.
View Solution

