Along the straight line joining two consecutive displacement nodes in a pure stationary sound wave at different points
the S.H.M's will be in different phases
Velocities are in phase
the accelerations are in phase
frequencies are equal
The correct Answer is:B, C, D
To solve the question regarding the behavior of particles along the straight line joining two consecutive displacement nodes in a pure stationary sound wave, we can break it down into the following steps:
1. Understanding Stationary Waves:
- In a stationary wave, there are points called nodes where there is no displacement of particles. Between these nodes, there are points called anti-nodes where the displacement is maximum.
Hint: Remember that nodes are points of zero displacement, while anti-nodes are points of maximum displacement.
2. Identifying Nodes and Anti-nodes:
- For a stationary sound wave, nodes occur at regular intervals along the wave. The distance between two consecutive nodes is half the wavelength (λ/2).
Hint: Visualize the wave to identify where nodes and anti-nodes are located.
3. Particle Motion Between Nodes:
- The particles between two consecutive nodes oscillate with varying amplitudes. The particles at the anti-nodes have maximum amplitude, while those closer to the nodes have smaller amplitudes.
Hint: Consider how the amplitude changes as you move from a node to an anti-node.
4. Direction of Motion:
- The particles on either side of a node move in opposite directions. For example, if one particle moves upward, the adjacent particle on the other side of the node moves downward.
Hint: Think about the symmetry of the wave and how particles interact around nodes.
5. Velocity and Acceleration:
- The velocities of particles at the same distance from the nodes but on opposite sides will be equal in magnitude but opposite in direction. Similarly, their accelerations will also be equal in magnitude and opposite in direction.
Hint: Use the concept of harmonic motion to understand how velocity and acceleration relate to displacement.
6. Frequency Consistency:
- All particles in the stationary wave oscillate with the same frequency, regardless of their position between nodes or anti-nodes.
Hint: Frequency is a property of the wave itself and remains constant throughout.
Final Conclusion
- Along the straight line joining two consecutive displacement nodes in a pure stationary sound wave, the particles exhibit oscillatory motion with varying amplitudes, opposite directions of motion on either side of the nodes, equal velocities and accelerations in magnitude but opposite in direction, and the same frequency.
- In a stationary wave, there are points called nodes where there is no displacement of particles. Between these nodes, there are points called anti-nodes where the displacement is maximum.
- For a stationary sound wave, nodes occur at regular intervals along the wave. The distance between two consecutive nodes is half the wavelength (λ/2).
- The particles between two consecutive nodes oscillate with varying amplitudes. The particles at the anti-nodes have maximum amplitude, while those closer to the nodes have smaller amplitudes.
- The particles on either side of a node move in opposite directions. For example, if one particle moves upward, the adjacent particle on the other side of the node moves downward.
- The velocities of particles at the same distance from the nodes but on opposite sides will be equal in magnitude but opposite in direction. Similarly, their accelerations will also be equal in magnitude and opposite in direction.
- All particles in the stationary wave oscillate with the same frequency, regardless of their position between nodes or anti-nodes.
- Along the straight line joining two consecutive displacement nodes in a pure stationary sound wave, the particles exhibit oscillatory motion with varying amplitudes, opposite directions of motion on either side of the nodes, equal velocities and accelerations in magnitude but opposite in direction, and the same frequency.
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-V (LEVEL-II(ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
2 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-V (LEVEL-II(ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
1 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-V (LEVEL-II(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
8 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
Knowledge Check
In a stationary longitudinal wave, nodes are points of
Aminimum displacement and minimum pressure change.Bminimum displacement and maximum pressure changeCmaximum displacement and maximum pressure changeDmaximum displacement and minimum pressure change.Two particles execute SHMs of the same amplitude and frequency along the same straight line. They cross one another when going in opposite direction. What is the phase difference between them when their displacements are half of their amplitudes ?
A60∘B30∘C120∘D150∘
What is the phase difference between the displacement wave and pressure wave in sound wave :-
View SolutionA standing wave in second overtone is maintained in a open pipe of length L. The distance between consecutive displacement node and pressure node is L/x. Find x
View SolutionA partial along a straight line whose velocity-displacement graph is as shown in the figure. What is the magnitude of acceleration when displacement is 3 m ?
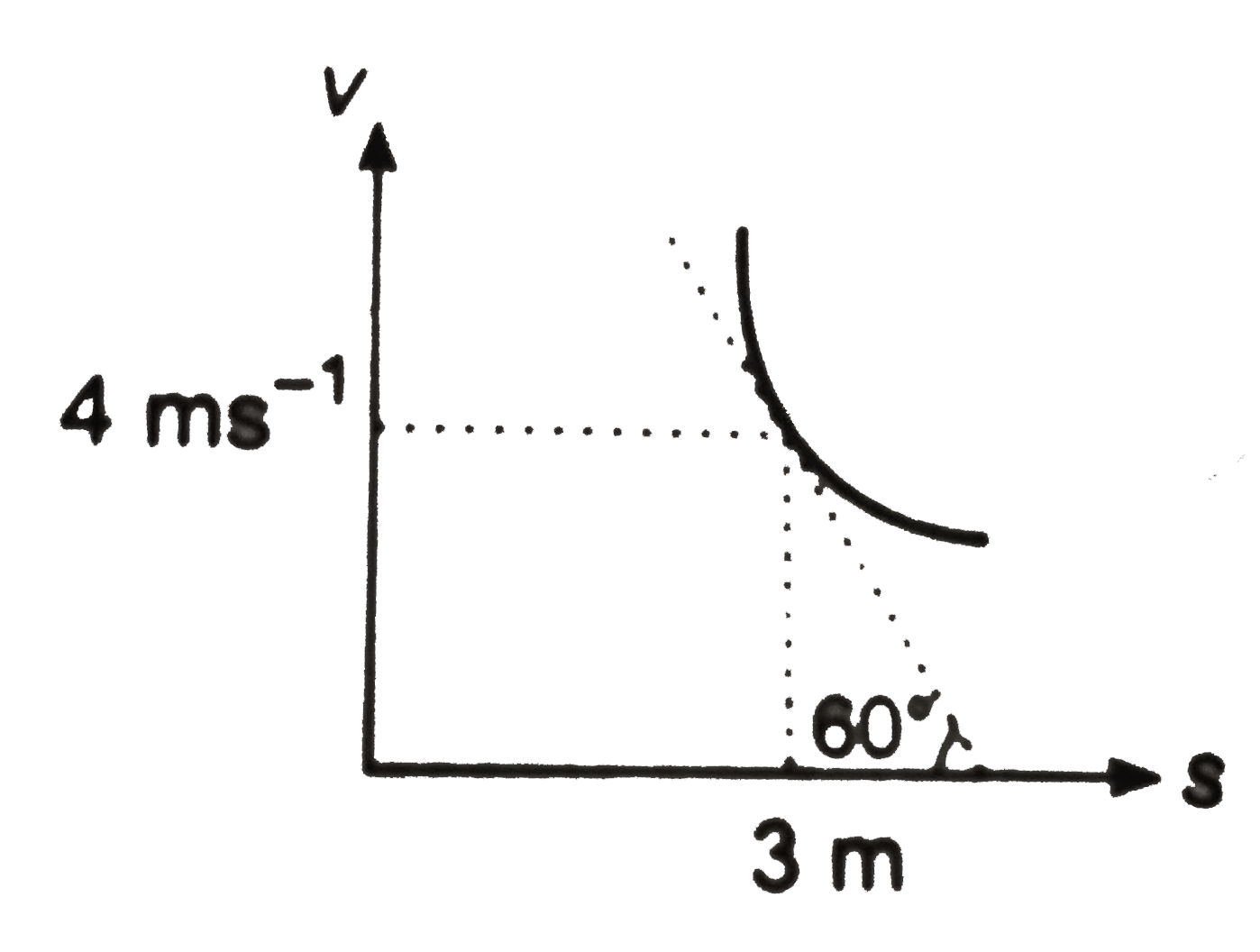
View SolutionA particle is moving along a straight line whose velocity - displacement graph is shown in figure. What is the acceleration when displacement is 3 m?
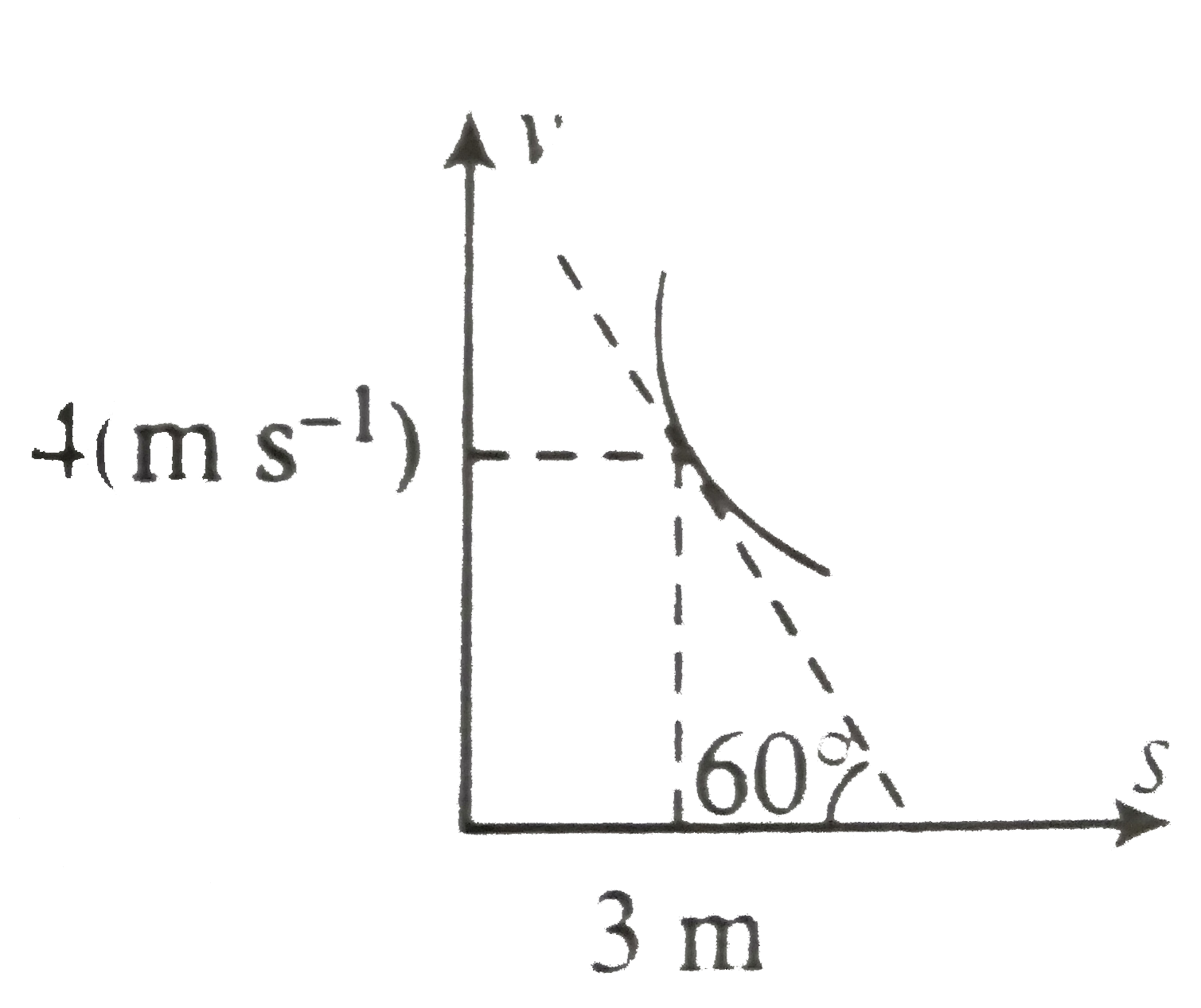
View SolutionFour points are such that the line joining any two points is perpendicular to the line joining other two points. If three point out of these lie on a rectangular hyperbola, then the fourth point will lie on
View SolutionShow that the straight line joining two variable points on an ellipse, whose eccentric angles differ by a constant, touch a concentric ellipse.
View Solution
