Question

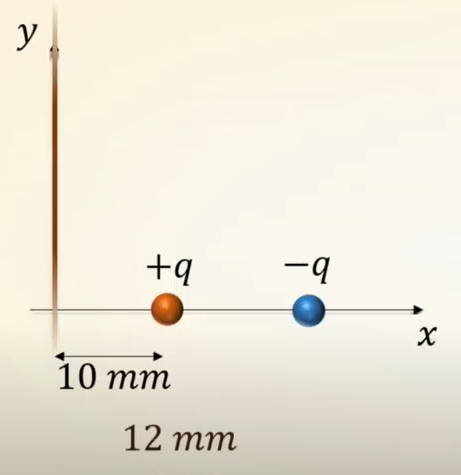
An electric dipole is placed on x-axis in proximity to a line charge of linear charge density $3.0\times {10}^{-6}$ C/m. Line charge is placed on z-axis and positive and negative charge of dipole is at a distance of 10 mm and 12 mm from the origin respectively. If total force of 4 N is exerted on the dipole, find out the amount of positive or negative charge of the dipole.

Options

A. `815.1 nC`
B. `8.8 muC`
C. `0.485mC`
D. `4.44 muC`

Explanation

To solve the problem, we need to find the amount of positive or negative charge of the electric dipole when it is placed near a line charge with a given linear charge density. Let's break down the solution step by step.

1. Understand the Configuration:
- The electric dipole consists of two charges, +Q and -Q, separated by a distance (d).
- The positive charge is at a distance of 10 mm from the origin (point P) and the negative charge is at a distance of 12 mm from the origin (point Q).
- The line charge with a linear charge density (λ) of \(3.0 \times 10^{-6} \, \text{C/m}\) is placed along the z-axis.

2. Calculate the Electric Field (E):
- The electric field (E) at point P due to the line charge can be calculated using the formula:
\( E = \frac{2k\lambda}{R} \)
- Here, \(k\) is Coulomb's constant (\(9 \times 10^9 \, \text{N m}^2/\text{C}^2\)), and \(R\) is the distance from the line charge to point P.
- The distance \(R\) is the x-coordinate of point P, which is 10 mm or \(10 \times 10^{-3} \, \text{m}\).

3. Determine the Force on Each Charge:
- The force on the positive charge (+Q) at point P is:
\( F_p = Q \cdot E = Q \cdot \frac{2k\lambda}{R} \)
- The force on the negative charge (-Q) at point Q is:
\( F_q = -Q \cdot E = -Q \cdot \frac{2k\lambda}{R + d} \)
- Here, \(d\) is the separation between the charges, which is \(2 \, \text{mm} = 2 \times 10^{-3} \, \text{m}\).

4. Calculate the Net Force (F_net):
- The net force on the dipole is given by:
\( F_{\text{net}} = F_p - F_q = Q \cdot \frac{2k\lambda}{R} - (-Q) \cdot \frac{2k\lambda}{R + d} \)
- Simplifying this gives:
\( F_{\text{net}} = 2k\lambda Q \left( \frac{1}{R} - \frac{1}{R + d} \right) \)

5. Substituting Known Values:
- We know \(F_{\text{net}} = 4 \, \text{N}\), \(\lambda = 3.0 \times 10^{-6} \, \text{C/m}\), \(k = 9 \times 10^9 \, \text{N m}^2/\text{C}^2\), \(R = 10 \times 10^{-3} \, \text{m}\), and \(d = 2 \times 10^{-3} \, \text{m}\).
- Substitute these values into the equation:
\( 4 = 2 \cdot (9 \times 10^9) \cdot (3.0 \times 10^{-6}) \cdot Q \left( \frac{1}{10 \times 10^{-3}} - \frac{1}{12 \times 10^{-3}} \right) \)

6. Calculate the Difference:
- Calculate the difference:
\( \frac{1}{10 \times 10^{-3}} - \frac{1}{12 \times 10^{-3}} = \frac{12 - 10}{120} = \frac{2}{120} = \frac{1}{60} \)

7. Final Calculation:
- Substitute back into the equation:
\( 4 = 2 \cdot (9 \times 10^9) \cdot (3.0 \times 10^{-6}) \cdot Q \cdot \frac{1}{60} \)
- Rearranging gives:
\( Q = \frac{4 \cdot 60}{2 \cdot (9 \times 10^9) \cdot (3.0 \times 10^{-6})} \)
- Calculate \(Q\):
\( Q = \frac{240}{54 \times 10^3} = \frac{240}{54000} \approx 4.44 \times 10^{-6} \, \text{C} \)

Conclusion:
The amount of positive or negative charge of the dipole is approximately \(4.44 \, \mu\text{C}\).