An ideal gas is enclosed in a cylinder with a movable piston on top of it. The piston has a mass of 800 g and an area of and is free slide up and down, keeping the pressure of the gas constant. How much work is done on the gas as the temperature of 0.200 mol of the gas is raised from to ?
To solve the problem, we need to calculate the work done on the gas as its temperature is raised at constant pressure. Here’s a step-by-step solution:
Step 1: Identify the given values
- Mass of the piston, m=800g=0.800kg
- Area of the piston, A=5.00cm2=5.00×10−4m2
- Number of moles of gas, n=0.200mol
- Initial temperature, Ti=20.0∘C=293.15K
- Final temperature, Tf=300.0∘C=573.15K
Step 2: Calculate the pressure exerted by the piston
Using the formula for pressure:
P=FA
where F=mg (the weight of the piston).
First, calculate the force:
F=m⋅g=0.800kg⋅9.81m/s2=7.848N
Now, calculate the pressure:
P=FA=7.848N5.00×10−4m2=15696Pa(or N/m2)
Step 3: Calculate the change in temperature
ΔT=Tf−Ti=573.15K−293.15K=280K
Step 4: Use the formula for work done at constant pressure
The work done on the gas can be calculated using the formula:
W=−PΔV
At constant pressure, we can use the ideal gas law:
ΔV=nRΔT/P
Substituting this into the work formula gives:
W=−nR(Tf−Ti)
Step 5: Substitute the values into the work formula
Using the ideal gas constant R=8.31J/(mol K):
W=−0.200mol⋅8.31J/(mol K)⋅280K
Calculating this gives:
W=−0.200⋅8.31⋅280=−466.08J
Final Answer
The work done on the gas is approximately:
W≈−466J
- Mass of the piston, m=800g=0.800kg
- Area of the piston, A=5.00cm2=5.00×10−4m2
- Number of moles of gas, n=0.200mol
- Initial temperature, Ti=20.0∘C=293.15K
- Final temperature, Tf=300.0∘C=573.15K
Using the formula for pressure:
P=FA
where F=mg (the weight of the piston).
F=m⋅g=0.800kg⋅9.81m/s2=7.848N
P=FA=7.848N5.00×10−4m2=15696Pa(or N/m2)
ΔT=Tf−Ti=573.15K−293.15K=280K
The work done on the gas can be calculated using the formula:
W=−PΔV
At constant pressure, we can use the ideal gas law:
ΔV=nRΔT/P
Substituting this into the work formula gives:
W=−nR(Tf−Ti)
Using the ideal gas constant R=8.31J/(mol K):
W=−0.200mol⋅8.31J/(mol K)⋅280K
Calculating this gives:
W=−0.200⋅8.31⋅280=−466.08J
The work done on the gas is approximately:
W≈−466J
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Solved Examples
14 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.1
20 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
An ideal gas is enclosed in a cyclinder with a movable piston on top. The piston has mass of 8000g and an area of 5.00cm2 and is free to slide up and down, keeping the pressure of the gas constant. How much work is done as the temperature of 0.200mol of the gas is raised from 200∘C to 300∘C?
View SolutionA cylinder has a movable piston on its top. The piston has a mass of 7 kg and an area of 6×10−4m2. The piston can slide up and down, keeping the pressure of the ideal gas enclosed in the cylinder constant. What is the work done if the temperature of 0.5 mol of the gas in raised from 30∘C to 250∘C?[R=8.31Jmol−1K−1]
View SolutionWhat will be the final pressure of an ideal gas present in a cylinder at 2 atm when the temperature of the gas is increased from 100∘C to 500∘C?
View SolutionBy the ideal gas law, the pressure of 0.60 mole NH3 gas in a 3.00 L vessel at 25∘C is
View SolutionSuppose there are N molecules each of mass m, of an ideal gas in a container. The x component of velocity of a molecule is denoted by ux. The gas is enclosed using a horizontal piston of area A as shown.

If the piston is moved so as to reduce the volume of gas by half, keeping the temperature of gas constant , we know from the gas law that the pressure will be doubled. On microscopic level the increase in pressure on the piston is because
View SolutionTwo moles of a gas at 8.21 bar and 300 K are expanded at constant temperature up to 2.73 bar against a constant pressure of 1 bar. How much work (in Latm) is done by the gas?
(neglect the sign)
View Solution2 moles of a diatomic gas are enclosed in a cylinder piston arrangment. The area of cross section and mass of the piston are 1cm2 and 1 kg respectively. A heater is supplying heat to the gas very slowly. Find heat supplied (in joule) by the heater is the piston moves through a distance of 10 cm.
 .
.
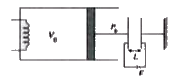
View SolutionAn ideal gas is enclosed in a cylinder fitted with a frictionless piston. The piston is connected with a light rod to one plate of capacitor whose other plate is fixed as shown. Initially volume of the gas inside the cylinder is V0 Atmospheric pressure is P0 separation between the plates is L, area of the piston as well as of the capacitor plates is A and emf of battery is ε . A heater supplies heat to the gas so that pressure of the gas is given as P=P0−nε0ε2L2 when piston is displaced by a distance L2 . Find value of n.
View SolutionTen dm3 of hydrogen under 1 bar pressure are contained in a cylinder which has a movable piston. The piston is moved in until the same mass of gas occupies 2dm3 at the same temperature. Find the pressure in the cylinder.
View SolutionOne mole of an ideal gas (Cv,m=52R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas is :
View Solution
