An Lc circuit contains a 40 mH inductor and a 25μF capacitor. The resistance of the circuit is negligible.The time is measured from the instant the circuit is closed. The energy stored in the circuit is completely magnetic at time (in milliseconds)
0,3.14,6.28
0,1.57,4.71
1.57,4.71,7.85
1.57,3.14,4.71
The correct Answer is:C
To solve the problem of finding the time at which the energy stored in an LC circuit is completely magnetic, we can follow these steps:
Step 1: Understand the LC Circuit
An LC circuit consists of an inductor (L) and a capacitor (C) connected in series. When the circuit is closed, energy oscillates between the capacitor and the inductor. The energy is stored as electric energy in the capacitor and as magnetic energy in the inductor.
Step 2: Identify the Given Values
- Inductance (L) = 40 mH = 40×10−3 H
- Capacitance (C) = 25 µF = 25×10−6 F
Step 3: Calculate the Frequency of Oscillation
The frequency of oscillation (f) in an LC circuit is given by the formula:
f=12π√LC
Substituting the values of L and C:
f=12π√(40×10−3)(25×10−6)
Step 4: Calculate the Period of Oscillation
The period (T) is the reciprocal of frequency:
T=1f
Substituting the expression for frequency:
T=2π√LC
Step 5: Substitute the Values to Find T
Calculating T:
T=2π√(40×10−3)(25×10−6)
Calculating the square root:
√(40×10−3)(25×10−6)=√1×10−6=10−3
Thus,
T=2π×10−3 seconds=2π milliseconds
Step 6: Determine the Time for Maximum Magnetic Energy
The energy in the inductor is maximum at specific times during the oscillation:
- This occurs at T/4,3T/4,5T/4,…
Substituting T=2π:
- First maximum: T/4=2π4=π2 milliseconds≈1.57 milliseconds
- Second maximum: 3T/4=3×2π4=3π2 milliseconds≈4.71 milliseconds
- Third maximum: 5T/4=5×2π4=5π2 milliseconds≈7.85 milliseconds
Step 7: Conclusion
The times at which the energy is completely magnetic are approximately:
- 1.57 ms
- 4.71 ms
- 7.85 ms
The correct answer is 1.57 ms, 4.71 ms, or 7.85 ms.
An LC circuit consists of an inductor (L) and a capacitor (C) connected in series. When the circuit is closed, energy oscillates between the capacitor and the inductor. The energy is stored as electric energy in the capacitor and as magnetic energy in the inductor.
- Inductance (L) = 40 mH = 40×10−3 H
- Capacitance (C) = 25 µF = 25×10−6 F
The frequency of oscillation (f) in an LC circuit is given by the formula:
f=12π√LC
Substituting the values of L and C:
f=12π√(40×10−3)(25×10−6)
The period (T) is the reciprocal of frequency:
T=1f
Substituting the expression for frequency:
T=2π√LC
Calculating T:
T=2π√(40×10−3)(25×10−6)
Calculating the square root:
√(40×10−3)(25×10−6)=√1×10−6=10−3
Thus,
T=2π×10−3 seconds=2π milliseconds
The energy in the inductor is maximum at specific times during the oscillation:
- This occurs at T/4,3T/4,5T/4,…
- First maximum: T/4=2π4=π2 milliseconds≈1.57 milliseconds
- Second maximum: 3T/4=3×2π4=3π2 milliseconds≈4.71 milliseconds
- Third maximum: 5T/4=5×2π4=5π2 milliseconds≈7.85 milliseconds
The times at which the energy is completely magnetic are approximately:
- 1.57 ms
- 4.71 ms
- 7.85 ms
Topper's Solved these Questions
Similar Questions
An L-C circuit contains 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0. what is the total energy stored initially ? At what times is the total energy shared equally between the inductor and the capacitor ?
View SolutionAn LC circuit contains a 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0.
(a) What is the total energy stored initially ? Is it conserved during the oscillalions?
(b) What is the natural frequency of the circuit?
(c ) At what time is the energy stored? (i) Completely electrical ? (ii) Completely magnetic ?
(d) At what time is the total energy shared equally between the inductor and the capacitor ?
(e) If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat ?
View Solution
Knowledge Check
An LC circuit contains a 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant at which the circuit which is closed be t=0. At what time the energy stored is completely magnetic ?
At = 0Bt=1.54msCt=3.14msDt=6.28msAn LC circuit contains a 20 mH inductor and 25μF capacitor with an initial charge of 5 mC. The total energy stored in the circuit initially is
A5 JB0.5JC50 JD500 J
In the steady state of the circuit shown in the figure the ratio of energy stored in the inductor to th energy stored in the capacitor is 1000000.
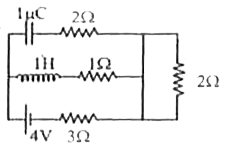
View SolutionIn the circuit as shown in figure, energy stored in capacitor at steady state is
View SolutionThe charge on 4μFcapacitor in the given circuit is (inμC)

View SolutionA series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
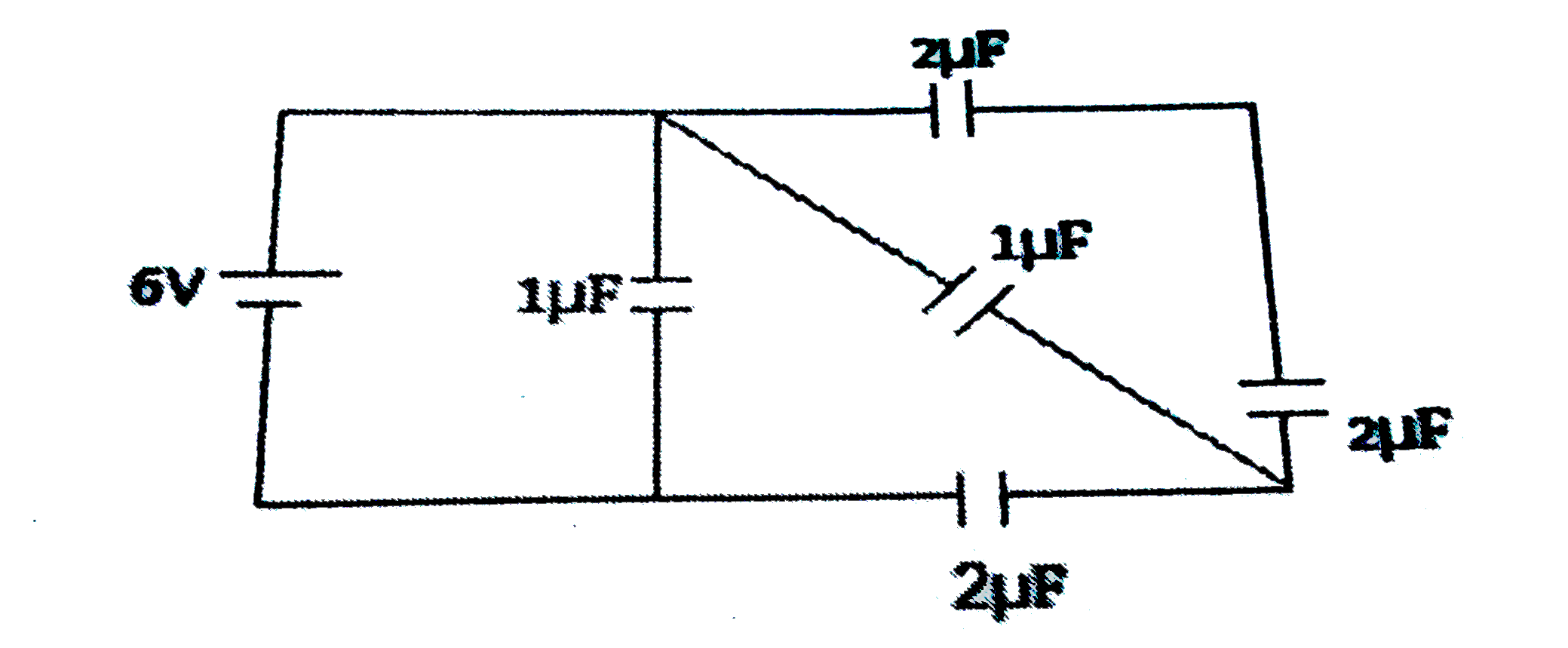
View SolutionFind total energy stored in capacitors given in the circuit
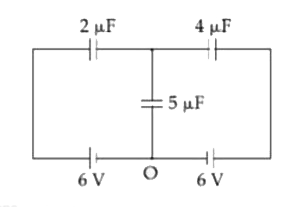
View SolutionIn the circuit shown , charge on the 5μF capacitor is :
View Solution
