An object is 30.0 cm form a spherical mirror, along the central axis.
The absolute value of lateral magnification is 12, The image produced is inverted .
What is the focal length of the mirror?
The correct Answer is:A, C
To solve the problem step by step, we will use the mirror formula and the magnification formula.
Step 1: Identify the given values
- Object distance (U) = -30 cm (the negative sign indicates that the object is in front of the mirror)
- Lateral magnification (|M|) = 1/2 (since the image is inverted, M will be negative)
Step 2: Use the magnification formula
The magnification (M) is given by the formula:
M=VU
Where:
- V = image distance
- U = object distance
Since the absolute value of magnification is given as 1/2, we can write:
−V30=−12
Step 3: Solve for V
From the magnification equation, we can rearrange it to find V:
V=12×U
Substituting U = -30 cm:
V=12×(−30)=−15 cm
Step 4: Use the mirror formula
The mirror formula is given by:
1F=1V+1U
Where F is the focal length.
Step 5: Substitute values into the mirror formula
Substituting V = -15 cm and U = -30 cm into the mirror formula:
1F=1−15+1−30
Step 6: Calculate the right-hand side
Calculating the right-hand side:
1F=−115−130
To add these fractions, we need a common denominator, which is 30:
1F=−230−130=−330=−110
Step 7: Solve for F
Taking the reciprocal gives:
F=−10 cm
Conclusion
The focal length of the mirror is -10 cm, indicating that it is a concave mirror.
---
- Object distance (U) = -30 cm (the negative sign indicates that the object is in front of the mirror)
- Lateral magnification (|M|) = 1/2 (since the image is inverted, M will be negative)
The magnification (M) is given by the formula:
M=VU
Where:
- V = image distance
- U = object distance
−V30=−12
From the magnification equation, we can rearrange it to find V:
V=12×U
Substituting U = -30 cm:
V=12×(−30)=−15 cm
The mirror formula is given by:
1F=1V+1U
Where F is the focal length.
Substituting V = -15 cm and U = -30 cm into the mirror formula:
1F=1−15+1−30
Calculating the right-hand side:
1F=−115−130
1F=−230−130=−330=−110
Taking the reciprocal gives:
F=−10 cm
The focal length of the mirror is -10 cm, indicating that it is a concave mirror.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise 30.12videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Introductory Exercise1videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Example Type 92videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary76videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Subjective21videos
REFRACTION OF LIGHT
Similar Questions
An object is 30.0 cm from a spherical mirror along the central axis. The absolute value of lateral magnification is 12. The image produced is inverted. What is the focal length of the mirror?
View SolutionAn object is 40 cm form a spherical mirror, along the central axis. The image produced is inverted. What is the power of the mirror?
View SolutionFor a plane mirror what is the focal length? The magnification?
View SolutionAn object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is
View SolutionWhen an object is placed at a distance of 40 cm from a concave mirror, the size of image is one fourth that of the object. A. Calculate the distance of image from the mirror b. What will be the focal length of the mirror?
View SolutionFor an object placed at a distance 20 cm from a concave mirror, the image is formed at the same position. What is the focal length of the mirror?
View SolutionA concave mirror gives a real image magnifies 4 times. When the object is moved 3 cm the magnification of the real image is 3 times. Find the focal length of mirror.
View SolutionAn object placed at 20cm in front of a concave mirror produces three times magnified real image. What is the focal length of the concave mirror?
View SolutionAn object kept on the principal axis and infront of a spherical mirror, is moved along the axis itself. Its lateral magnification m is measured, and plotted versus object distance |u| for a range of u, as shown in figure. The magnification of the object when it is placed at a distance 20cm in front of the mirror is
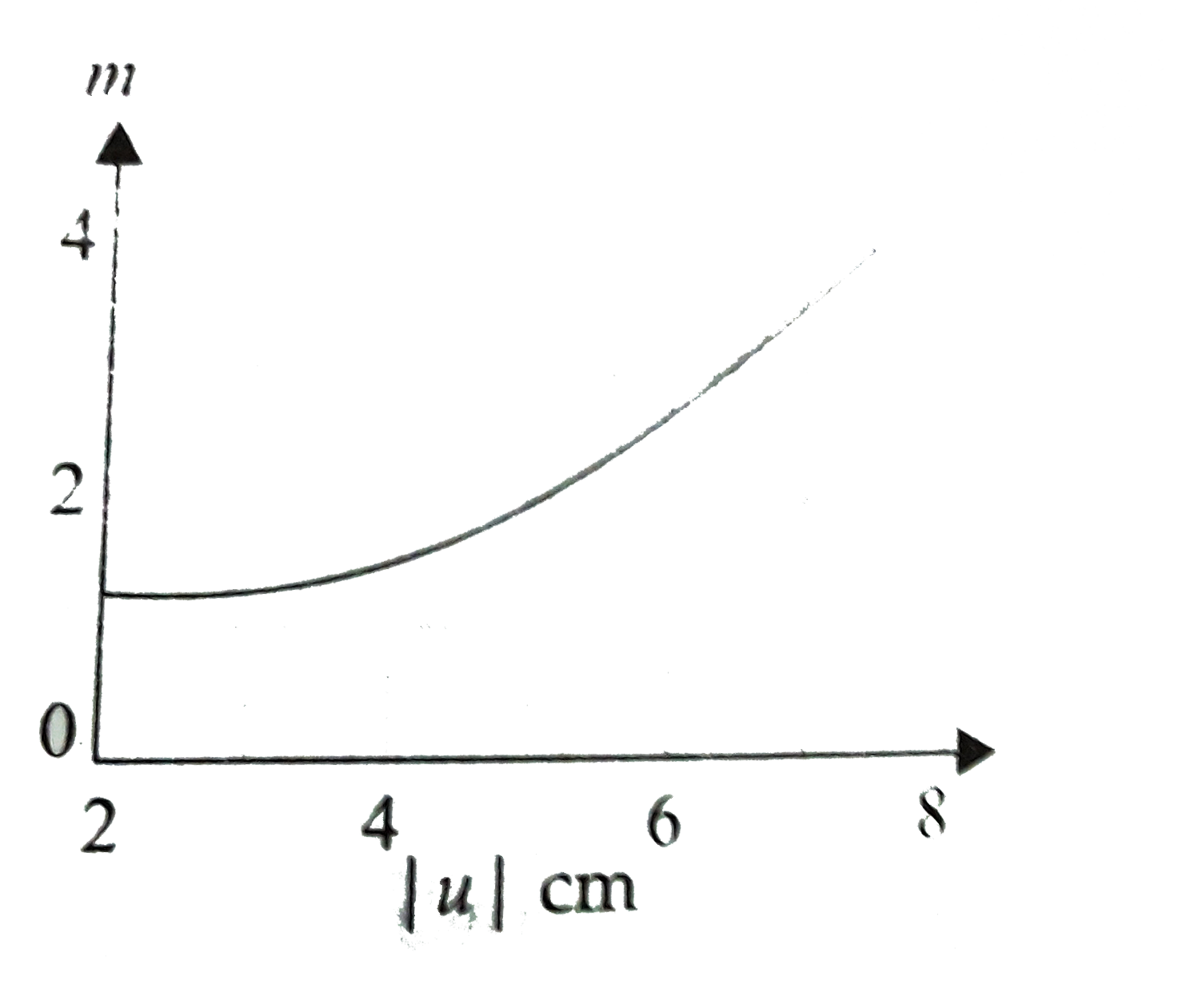 View Solution
View SolutionA spherrical mirror forms an erect image three times the size of the object, If the distance between the object and the inage is 80 cm. The nature and the focal length of the mirror are
View Solution
