An object is put at a distance of 5cm from the first focus of a convex lens of focal length 10cm. If a real image is formed, its distance from the lens will be
15cm
20cm
25cm
30cm
The correct Answer is:d.
To solve the problem, we will use the lens formula for a convex lens, which is given by:
1f=1v−1u
Where:
- f is the focal length of the lens,
- v is the image distance from the lens,
- u is the object distance from the lens.
Step 1: Identify the given values
From the problem, we have:
- Focal length f=10cm (for a convex lens, this is positive),
- Object distance u=−5cm (the object is placed on the same side as the incoming light, hence negative).
Step 2: Substitute the values into the lens formula
Using the lens formula:
1f=1v−1u
Substituting the values of f and u:
110=1v−1−5
Step 3: Simplify the equation
This can be rewritten as:
110=1v+15
To combine the fractions on the right side, we need a common denominator. The common denominator between v and 5 is 5v:
110=5+v5v
Step 4: Cross-multiply to solve for v
Cross-multiplying gives:
5v⋅110=5+v
This simplifies to:
5v10=5+v
or
v2=5+v
Step 5: Rearranging the equation
Rearranging gives:
v2−v=5
This can be rewritten as:
−v2=5
Multiplying both sides by -2 gives:
v=−10
Step 6: Solve for v
Now, substituting back into the equation:
v=30cm
Conclusion
The distance of the real image from the lens is v=30cm.
- f is the focal length of the lens,
- v is the image distance from the lens,
- u is the object distance from the lens.
From the problem, we have:
- Focal length f=10cm (for a convex lens, this is positive),
- Object distance u=−5cm (the object is placed on the same side as the incoming light, hence negative).
Using the lens formula:
This can be rewritten as:
Cross-multiplying gives:
Rearranging gives:
Now, substituting back into the equation:
The distance of the real image from the lens is v=30cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
Knowledge Check
An object is kept at a distance of 15 cm from a convex lens of focal length 10 cm. Calculate the image distance and state the characteristics of the image formed.
Aupright and magnifiedBinverted and magnifiedCinverted and diminishedDupright and diminishedAn object of height 1.5 cm is placed on the axis of a convex lens of focal length 25 cm . A real image is formed at a distance of 75 cm from the lens. The size of the image will be
A4.5 cmB3.0 cmC0.75 cmD0.5 cmAn object is placed at a distance of 20 cm from a convex lens of focal length 10 cm . The image is formed on the other side of the lens at a distance
A20 cmB10 cmC40 cmD30 cm
Point object O is placed at a distance of 20cm from a convex lens of focal length 10cm as shown in Figure., At what distance x from the lens should a concave mirror of focal length 60cm, be placed so that the final image coincides with the object?
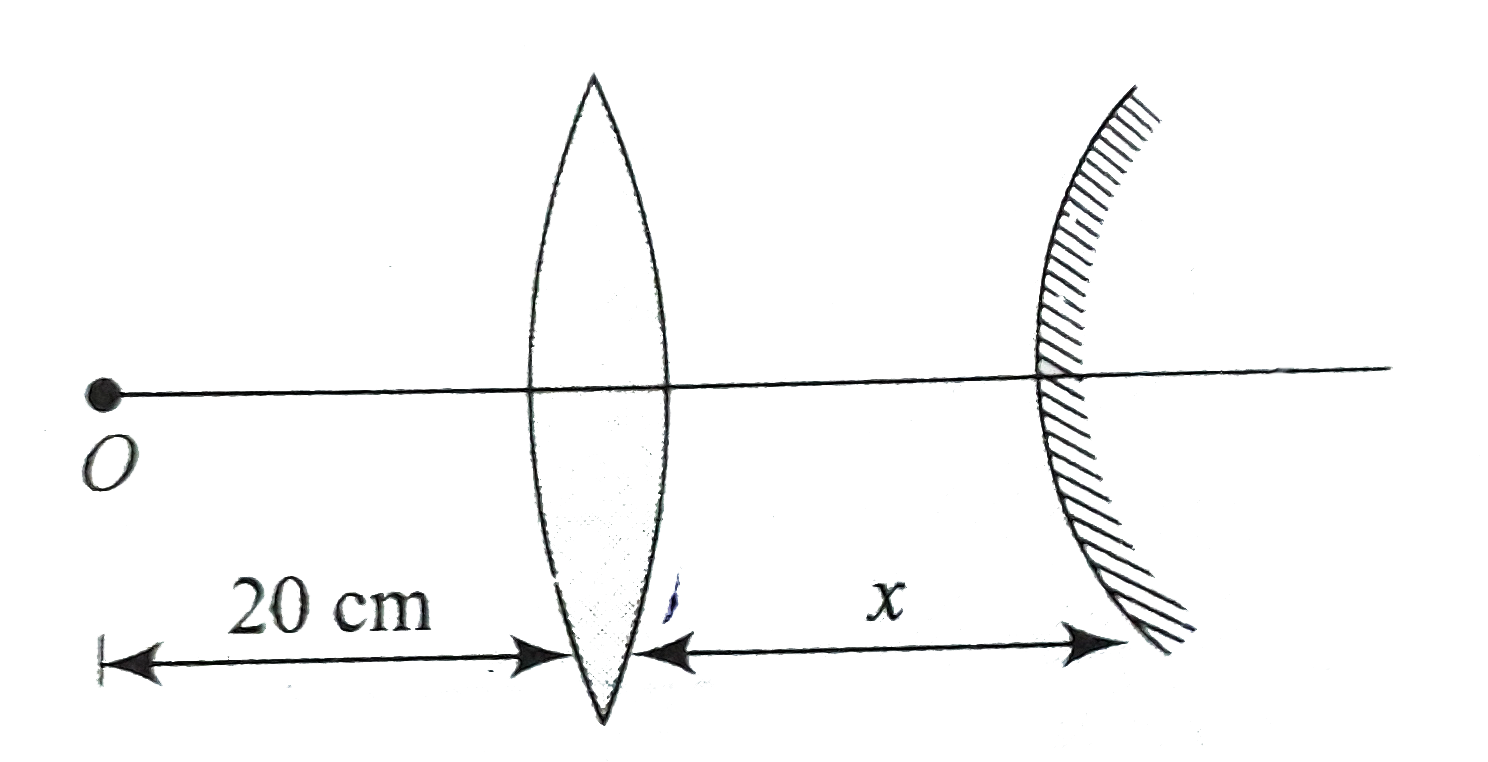
View SolutionAn object is kept at a distance of 60 cm in front of a convex lens. Its real and inverted image is fonned at a distance of 20 cm from the lens. Find the focal length of the lens.
View SolutionAn object is placed at 10 cm from a convex lens of focal length 12 cm. Find the position, nature and magnification of the image.
View SolutionAn object placed at a distance of a 9cm from the first principal focus of a convex lens produces a real image at a distance of 25cm. from its second principal focus. then the focal length of the lens is :
View SolutionAn object is placed at f/2 away from first focus of a convex lens where f is the focal length of the lens. Its image is formed at a distance 3f/2 in a slab of refractive index 3/2 , from the face of the slab facing the lens. Find the distance of this face of the slab from the second focus of the lens.
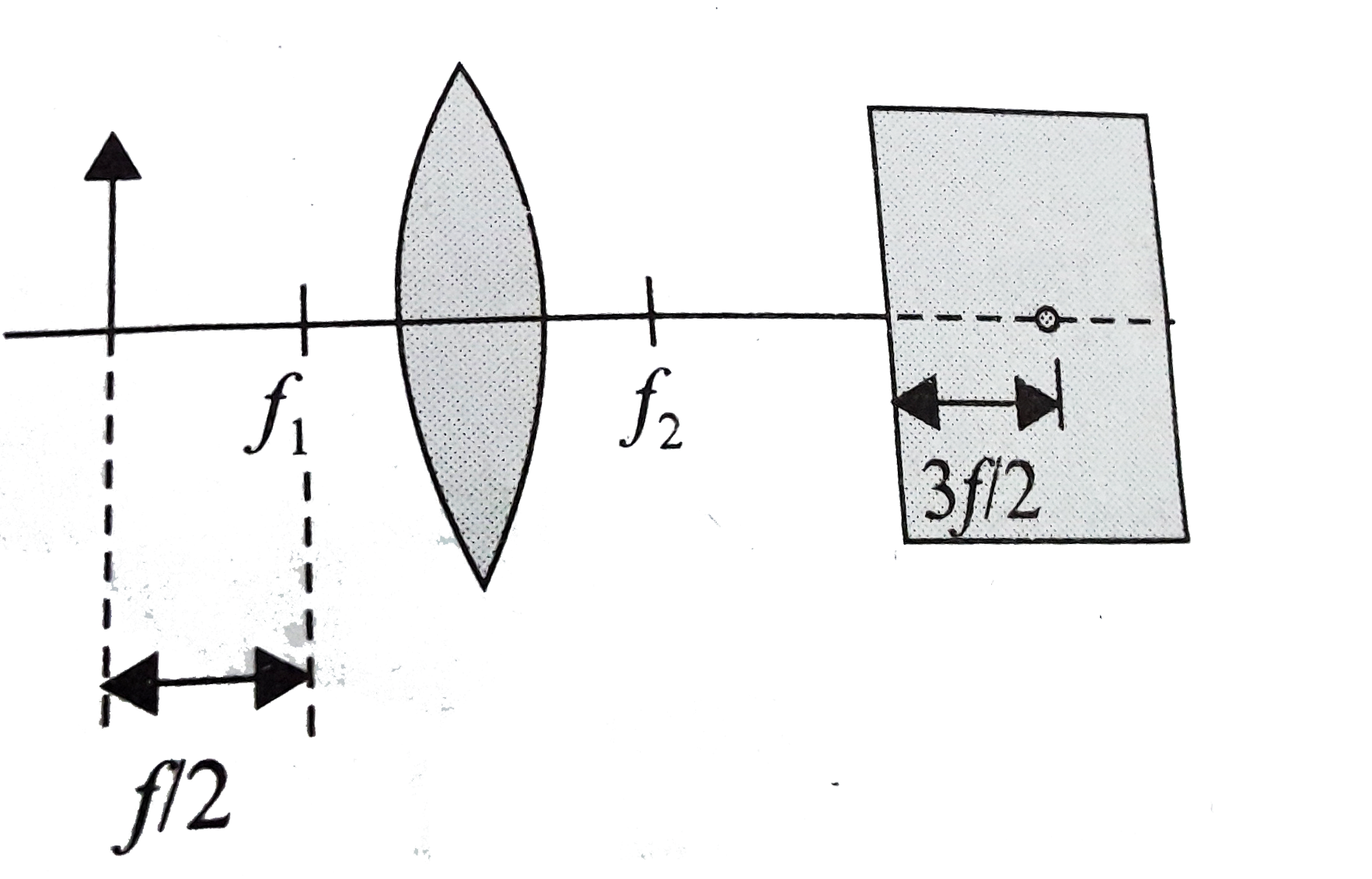
View Solution
