Assertion : The amplitude of oscillation can never be infinite. lt brgt Reason : The energy of oscillator is continuously dissipated.
If both assertion and reason are true and the reason is the correct explanation of the assertion.
If both assertion and reason are true but reason is not the correct explanation of the assertion.
If assertion is true but reason is false.
If the assertion and reason both are false
The correct Answer is:A
From equation, amplitude of oscillation
A=F0/m√(ω2−ω20)2+(bω/m)2
In absence of damping force (b=0), that the steady state amplitude approaches infinity as ω→ω0.
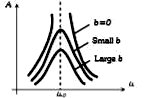 .
.
That is, if there is no resistive force in the system and
then it is possible to drive an oscillator with sinusoidal
force at the resonance frequency, the amplitude of
motion will build up without limit. This does not occur
in practice because some damping is always present in
real oscillation.
Topper's Solved these Questions
Similar Questions
In dampled oscillations, the amplitude of oscillation is reduced to one-third of its initial value of 9cm at the end of 100 oscillations. What will be its amplitude of oscillation in cm when it completes 200 oscillations.
View SolutionIn dampled oscillations, the amplitude of oscillatinos is reduced to one-fourth of its initial value 10cm at the end of 50 oscillations. What will be its amplitude when the oscillator completes 150 oscillations ?
View Solution
Knowledge Check
- Question 1 - Select One
At resonance the amplitude of forced oscillations is
AminimumBmaximumCzeroDNone of these - Question 2 - Select One
At resonance, the amplitude of forced oscillations is
AminimumBmaximumCzeroDnone of these - Question 3 - Select One
Vibrations, whose amplitudes of oscillations decrease with time, are called
Afree vibrationsBforced vibrationsCdamped vibrationsDnone of these
In the given table, Column I gives type of oscillation, Column II gives change in amplitude of oscillation and Column III gives examples of these types of oscillation.

The combination that defines the features of damped oscillation isView SolutionThe kinetic energy of a particle executing SHM is 16J. When it is in its mean position. If the amplitude of oscillation is 25cm and the mass of the particle is 5.12 kg, the itme period of its oscillation in second is
View SolutionAssertion : In x-=3+4 cosωt , amplitude of oscillation is 4 units.
Reason : Mean position is at x=3.View SolutionAssertion : For an oscillating simple pendulum, the tension in the string is maximum at the mean position and minimum at the extreme position. lt brgt Reason : The velocity of oscillating bob in simple harmonic motion is maximum at the mean position.
View SolutionAssertion: If the amplitude of a simple harmonic oscillator is doubled, its total energy becomes double.
Reason: The toal energy is directly proportional to the amplitude of vibration of the harmonic oscillator.View Solution

