Assertion : Total flux through a closed surface is zero if no charge is enclosed by the surface.
Reason : Gauss law is true for any closed surface, no matter what its shape or size is.
If both assertion and reason are true and reason is the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:B
To solve the given question, we need to analyze both the assertion and the reason provided.
Step 1: Understanding the Assertion
The assertion states that "Total flux through a closed surface is zero if no charge is enclosed by the surface." According to Gauss's law, the electric flux (Φ) through a closed surface is given by the equation:
Φ=Qencϵ0
where Qenc is the total charge enclosed by the surface and ϵ0 is the permittivity of free space. If there is no charge enclosed (Qenc=0), then:
Φ=0ϵ0=0
Thus, the assertion is true.
Step 2: Understanding the Reason
The reason states that "Gauss law is true for any closed surface, no matter what its shape or size is." Gauss's law applies universally to all closed surfaces, regardless of their geometry. This means that the law holds true for spherical, cylindrical, or any arbitrary closed surfaces. Therefore, this statement is also true.
Step 3: Analyzing the Relationship
While both the assertion and the reason are true, we need to determine if the reason correctly explains the assertion. The assertion is specifically about the condition of having no charge enclosed leading to zero flux, while the reason discusses the general applicability of Gauss's law. Therefore, the reason does not directly explain why the total flux is zero when no charge is enclosed.
Conclusion
Both the assertion and the reason are true, but the reason is not a correct explanation for the assertion. Thus, the correct answer is that both statements are true, but the reason is not a correct explanation for the assertion.
Final Answer
- Assertion: True
- Reason: True, but not a correct explanation for the assertion.
The assertion states that "Total flux through a closed surface is zero if no charge is enclosed by the surface." According to Gauss's law, the electric flux (Φ) through a closed surface is given by the equation:
Φ=Qencϵ0
where Qenc is the total charge enclosed by the surface and ϵ0 is the permittivity of free space. If there is no charge enclosed (Qenc=0), then:
Φ=0ϵ0=0
Thus, the assertion is true.
The reason states that "Gauss law is true for any closed surface, no matter what its shape or size is." Gauss's law applies universally to all closed surfaces, regardless of their geometry. This means that the law holds true for spherical, cylindrical, or any arbitrary closed surfaces. Therefore, this statement is also true.
While both the assertion and the reason are true, we need to determine if the reason correctly explains the assertion. The assertion is specifically about the condition of having no charge enclosed leading to zero flux, while the reason discusses the general applicability of Gauss's law. Therefore, the reason does not directly explain why the total flux is zero when no charge is enclosed.
Both the assertion and the reason are true, but the reason is not a correct explanation for the assertion. Thus, the correct answer is that both statements are true, but the reason is not a correct explanation for the assertion.
- Assertion: True
- Reason: True, but not a correct explanation for the assertion.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Electric Charges
5 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Charging By Induction
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
Knowledge Check
The net magnetic flux through any closed surface, kept in a magnetic field is
AzeroBμ04πC4πμ0D4μ0π
The net magnetic flux through any closed surface, kept in a magnetic field is
View SolutionIf the flux of the electric field through a closed surface is zero,
View SolutionA closed surface encloses a net charge of −3.60μC. What is the net electric flux through the surface?
(b) The electric flux through a closed surface is found to be 780N−m2/C. What quantity of charge is enclosed by the surface?
(c) The closed surface in part (b) is a cube with sides of length 2.50 cm. From the information given in part (b), is it possible to tell where within the cube the charge is located? Explain.
View Solution(a) define electrie flux. Write its, S.I unit.
" Gauses's law in electrostatis is true for any closed surface, no matter what its shape or size is.
Justify this statement with the help of a suitable example.
(b) Use Gauss's law to prove that the electric field inside a uniformly charged spherical shell is zero.
View Solution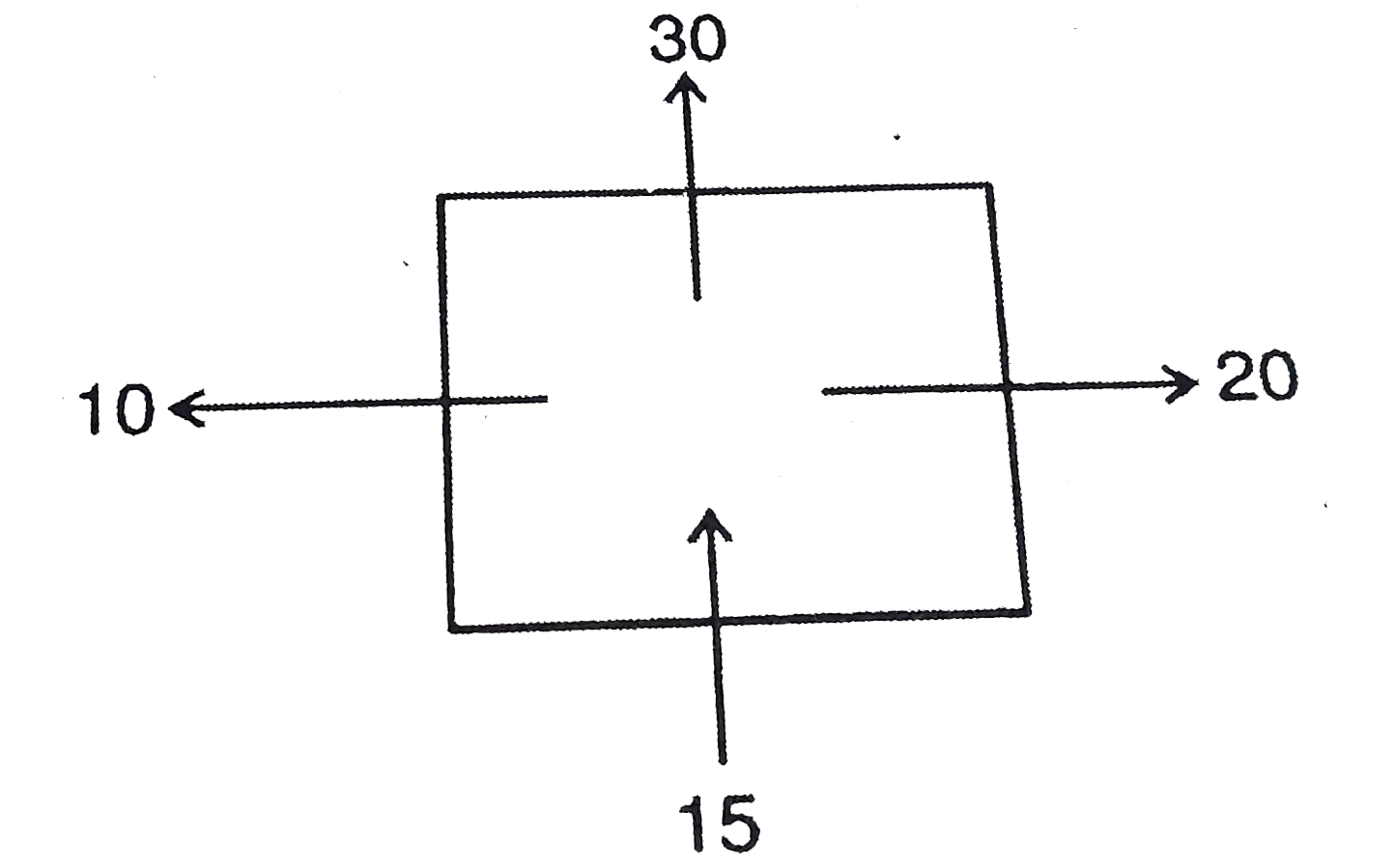
Flux (in S.I. units) coming out and eantering a closed surface is shown in the figure. Find charge enclosed by the closed surface.
View SolutionIf the number of electric lines of force emerging out of a closed surfsace is 1000, then the charge enclosed by the surface is
View SolutionThis question contains Statement -1 and Stantement -2 Of the four choices given after the statements, choose the one that best desctibes the two statemesnts.
Statement -1:
For a mass M kept at the center of a cube of side 'a', the flux of gravitational field passing through its sides 4πGM.
Statement -2:
If the direction of a field due to a point source is radial and its dependence on the distance 'r' from the source is given as 1r2, its flux through a closed surface depends only on the strength of the source enclosed by the surface and not on the size or shape of the surface.
View Solution
